Graphics class and Transformation in GDI+

This article has been excerpted from book "Graphics Programming with GDI+".

Before we move to other transformation related classes, let's review the transformation functionality defined in the Graphics class, as described in Table 10.2. We will see how to use these members in the examples throughout this article.

The Transform property of the Graphics class represents the world transformation of a Graphics object. It is applied to all items of the object. For example, if you have a rectangle, an ellipse, and a line and set the

TABLE 10.2: Transformation-related members defined in the Graphics class

Member	Description
MultiplyTransform	Method that multiplies the world transformation of a Graphics object and a Matrix object. The Matrix object specifies the transformation action (scaling, rotation, or translation).
ResetTransform	Method that resets the world transformation matrix of a Graphics object to the identity matrix.
RotateTransform	Method that applies a specified rotation to the transformation matrix of a Graphics object.
ScaleTransform	Method that applies a specified scaling operation to the transformation matrix of a Graphics object by prepending it to the object's transformation matrix.
Transform	Property that represents the world transformation for a Graphics object. Both get and set.
TransformPoints	Method that transforms an array of points from one coordinates space to another using the current world and page transformations of a Graphics object.
TranslateClip	Method that translates the clipping region of a Graphics object by specified amounts in the horizontal and vertical directions.
TranslateTransform	Method that prepends the specified translation to the transformation matrix of a Graphics object.

Transform property of the Graphics object, it will be applied to all three items. The Transform property is a Matrix object. The following code snippet creates a Matrix object and sets the Transform property:

            Matrix X = new Matrix();
            X.Scale(2, 2, MatrixOrder.Append);
            g.Transform = X;

The transformation methods provided by the Graphics class are MultiplyTransform, ResetTransform, RotateTransform, ScaleTransform, TransformPoints, TranslateClip, and TranslateTransform. The MultiplyTransform method multiplies a transformation matrix by the world transformation coordinates of a Graphics object. It takes an argument of Matrix type. The second argument, which specifies the order of multiplication operation, is optional. The following code snipped creates a Matrix object with the Translate transformation. The MultiplyTransform method multiplies the Matrix object by the world coordinates of the Graphics object, translating all graphics items drawn by the Graphics object.

            Matrix X = new Matrix();
            X.Translate(200.0f, 100.0f);
            g.MultiplyTransform(X, MatrixOrder.Append);

RotateTransform rotates the world transform by a specified angle. This method takes a floating point argument, which represents the rotation angle, and an optional second argument of MatrixOrder. The following code snippet rotates the world transformation of the Graphics object by 45 degrees:

            g.RotateTransform(45, 0f, MatrixOrder.Append);

The ScaleTransform method scales the world transformation in the specified x- and y-directions. The first and second arguments of this method are x- and y-directions scaling factors, and the third optional argument is MatrixOrder. The following code snipped scales the world transformation by 2 in the x-direction and 3 in the y-direction.

            g.ScaleTransform(2.0f, 3.0f, MatrixOrder.Append);

The TranslateClip method translates the clipping region in the horizontal and vertical directions. The first argument of this method represents the translation in the x-direction, and the second argument represents the translation in the y-direction:

            e.Graphics.TranslateClip(20.0f, 10.0f);

The TranslateTransform method translates the world transformation by the specified x- and y-values and takes an optional third argument of MatrixOrder:

            g.TranslateTransform(100.0f, 0.0f, MatrixOrder.Append);

We will use all of these methods in our examples.

Global, Local and Composite Transformations

Transformation can be divided into two categories based on their scope: global and local. In addition, there are composite transformations. A global transformation is applicable to all items of a Graphics object. The Transform property of the Graphics class is used to set global transformations.

A composite transformation is a sequence of transformations. For example, scaling followed by translation and rotation is a composite translation. The MultiplyTransform, RotateTransform, ScaleTransform, and TranslateTransform methods are used to generate composite transformations.

Listing 10.14 draws two ellipses and a rectangle, then call ScaleTransform, TranslateTransform, and RotateTransform (a composite transformation). The items are drawn again after the composite transformation.

LISTING 10.14: Applying composite transformation

        private void Form1_Paint(object sender, PaintEventArgs e)
        {
            //Create a Graphics object
            Graphics g = this.CreateGraphics();
            g.Clear(this.BackColor);
            //Create a blue pen with widht of 2
            Pen bluePen = new Pen(Color.Blue, 2);
            Point pt1 = new Point(10, 10);
            Point pt2 = new Point(20, 20);
            Color[] LnColors = { Color.Black, Color.Red };
            Rectangle rect1 = new Rectangle(10, 10, 15, 15);
            //Create two linear gradient brushes
            LinearGradientBrush LgBrush1 = new LinearGradientBrush
                (rect1, Color.Blue, Color.Green,
                LinearGradientMode.BackwardDiagonal);
            LinearGradientBrush LgBrush = new LinearGradientBrush
                (pt1, pt2, Color.Red, Color.Green);
            //Set linear colors
            LgBrush.LinearColors = LnColors;
            //Set gamma correction
            LgBrush.GammaCorrection = true;
            //fill and draw rectangle and ellipses
            g.FillRectangle(LgBrush, 150, 0, 50, 100);
            g.DrawEllipse(bluePen, 0, 0, 100, 50);
            g.FillEllipse(LgBrush1, 300, 0, 100, 100);
            //Apply scale transformation
            g.ScaleTransform(1, 0.5f);
            //Apply translate transformation
            g.TranslateTransform(50, 0, MatrixOrder.Append);
            //Apply rotate transformation
            g.RotateTransform(30.0f, MatrixOrder.Append);
            //Fill Ellipse
            g.FillEllipse(LgBrush1, 300, 0, 100, 100);
            //Rotate again
            g.RotateTransform(15.0f, MatrixOrder.Append);
            //Fill rectangle
            g.FillRectangle(LgBrush, 150, 0, 50, 100);
            //Rotate again
            g.RotateTransform(15.0f, MatrixOrder.Append);
            //Draw ellipse
            g.DrawEllipse(bluePen, 0, 0, 100, 50);
            //Dispose of objects
            LgBrush1.Dispose();
            LgBrush.Dispose();
            bluePen.Dispose();
            g.Dispose();
        }

Figure 10.15 shows the output from Listing 10.14.

A local transformation is applicable to only a specific item of a Graphics object. The best example of local transformation is transforming a graphics path. The Translate method of the GraphicsPath class translates only the items of a graphics path. Listing 10.15 translates a graphics path. We create a Matrix object and apply rotate and translate transformation to it.



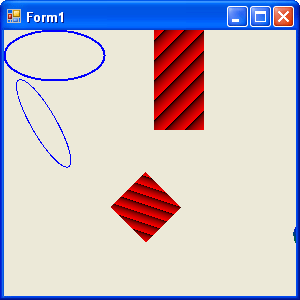
FIGURE 10.15: Composite transformation

LISTING 10.15: Translating graphics path items.

        private void Form1_Paint(object sender, PaintEventArgs e)
        {
            //Create a Graphics object
            Graphics g = this.CreateGraphics();
            g.Clear(this.BackColor);
            //Create a GraphicsPAth object
            GraphicsPath path = new GraphicsPath();
            //Add an ellipse and a line to the graphics path
            path.AddEllipse(50, 50, 100, 150);
            path.AddLine(20, 20, 200, 20);
            //Create a blue pen with a width of 2
            Pen bluePen = new Pen(Color.Blue, 2);
            //Create a Matrix object
            Matrix X = new Matrix();
            //Rotate 30 degrees
            X.Rotate(30);
            //Translate with 50 offset in x direction
            X.Translate(50.0f, 0);
            //Apply transformation on the path
            path.Transform(X);
            //Draw a rectangle, a line and the path
            g.DrawRectangle(Pens.Green, 200, 50, 100, 100);
            g.DrawLine(Pens.Green, 30, 20, 300, 20);
            g.DrawPath(bluePen, path);
            //Dispose of objects
            bluePen.Dispose();
            path.Dispose();
            g.Dispose();
        }
    }

Figure 10.16 shows the output from Listing 10.15. The transformation affects only graphics path items (the ellipse and the blue [dark] line).



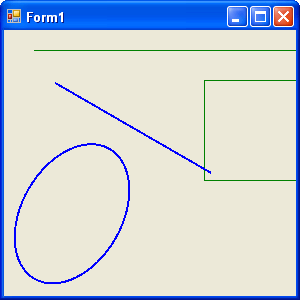
FIGURE 10.16: Local transformation

Conclusion

Hope the article would have helped you in understanding Graphics class and Transformation in GDI+. Read other articles on GDI+ on the website.

This book teaches .NET developers how to work with GDI+ as they develop applications that include graphics, or that interact with monitors or printers. It begins by explaining the difference between GDI and GDI+, and covering the basic concepts of graphics programming in Windows.