This article has been excerpted from book "Graphics Programming with GDI+".
The ScaleTransform, RotateTransform, and TranslateTransform methods to transform text. We can also use a transformation matrix to transform text.
We create a Matrix object with the transformation properties and apply it to the surface using the Transform property of the Graphics object. Listing 10.21 creates a Matrix object and sets it as the Transform property. We then call DrawString, which draws the text on the form. To test this code, add the code to a form's paint event handler.
LISTING 10.21: Text transformation example
Graphics g = e.Graphics;
string str =
"Colors, fonts, and text are common" +
" elements of graphics programming." +
"In this article, you learned " +
" about the colors, fonts and text" +
" representations in the " +
" .NET Framework class library. " +
"You learned how to create " +
"these elements and use them in GDI+. ";
//Create a Matrix object
Matrix M = new Matrix(1, 0, 0.5f, 1, 0, 0);
g.RotateTransform(45.0f,
System.Drawing.Drawing2D.MatrixOrder.Prepend);
g.TranslateTransform(-20, -70);
g.Transform = M;
g.DrawString(str,
new Font("Verdana", 10),
new SolidBrush(Color.Blue),
new Rectangle(50, 20, 200, 300));
Figure 10.30 shows the outcome of Listing 10.21.

FIGURE 10.30: Using the transformation matrix to transform text
We can apply shearing and other effects by changing the values of Matrix. For example, if we change Matrix as follows:
Matrix M = new Matrix(1, 0.5f, 0, 1, 0, 0);
the new code will generate Figure 10.31.
We can reverse the text just by changing the value of the Matrix object as follows:
Matrix M = new Matrix(1, 1, 1, -1, 0, 0);
with the result shown in Figure 10.32.
The Significance of Transformation Order
The Matrix object can store a single transformation or a sequence of transformations. As we learned in Section 10.5, a sequence of transformations. As we learned in Section 10.5, a sequence of transformations is called a composite transformation, which is a result of multiplying the matrices of the individual transformations.
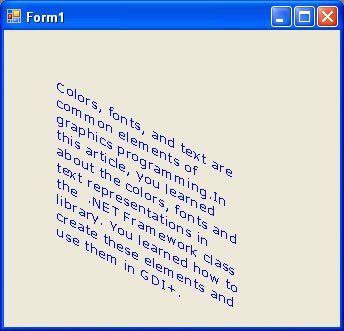
FIGURE 10.31: Using the transformation matrix to shear text

FIGURE 10.32: Using the transformation matrix to reverse text
In a composite transformation the order of the individual transformation is very important. Matrix operations are not cumulative. For example the result of a Graphics -> Rotate -> Translate -> Scale -> Graphics operation will be different from the result of a Graphics -> Scale -> Rotate -> Translate -> Graphics operation. The main reason that order is significant is that transformation like rotation and scaling are done with respect to the origin of the coordinate system. The result of scaling an object that is centered at the origin is different from the result of scaling an object that has been moved away from the origin. Similarly the result of rotating an object that is centered at the origin is different from the result of rotating an object that has been moved away from the origin.
The MatrixOrder enumeration, which is an argument to the transformation methods, represents the transformation order. It has two values: Append and Prepend.
Let's write an application to see how transformation order works. We create a Windows application and add a MainMenu control and three menu items to the form. The MatrixOrder class is defined in the System.Drawing.Drawing2D namespace, so we also add a reference to this namespace.
Listing 10.22 draws a rectangle before and after applying a Scale -> Rotate -> Translate transformation sequence.
LISTING 10.22: Scale -> Rotate -> Translate transformation order
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Drawing.Drawing2D;
using System.Text;
using System.Windows.Forms;
namespace Text_Transformation
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void Form1_Paint(object sender, PaintEventArgs e)
{
//Create a Graphics object
Graphics g = this.CreateGraphics();
g.Clear(this.BackColor);
//Create a rectangle
Rectangle rect =
new Rectangle(20, 20, 100, 100);
//Create a solid brush
SolidBrush brush =
new SolidBrush(Color.Red);
//Fill Rectangle
g.FillRectangle(brush, rect);
//Scale
g.ScaleTransform(1.75f, 0.5f);
//rotate
g.RotateTransform(45.0f, MatrixOrder.Append);
//Translate
g.TranslateTransform(150.0f, 50.0f, MatrixOrder.Append);
//Fill rectangle again
g.FillRectangle(brush, rect);
//Dispose of objects
brush.Dispose();
g.Dispose();
}
}
}
Figure 10.33 shows the output from Listing 10.22. The original rectangle is in the upper left; on the lower right is the rectangle after composite transformation.
Now let's change the order of transformation to Translate -> Rotate -> Scale with Append, as shown in Listing 10.23.

FIGURE 10.33: Scale ->Rotate -> Translate composite transformation
LISTING 10.23: Translate -> Rotate -> Scale transformation order with append
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Drawing.Drawing2D;
using System.Text;
using System.Windows.Forms;
namespace Text_Transformation
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void Form1_Paint(object sender, PaintEventArgs e)
{
//Create a Graphics object
Graphics g = this.CreateGraphics();
g.Clear(this.BackColor);
//Create a rectangle
Rectangle rect =
new Rectangle(20, 20, 100, 100);
//Create a solid brush
SolidBrush brush =
new SolidBrush(Color.Red);
//Fill Rectangle
g.FillRectangle(brush, rect);
//Translate
g.TranslateTransform(100.0f, 50.0f,
MatrixOrder.Append);
//Scale
g.ScaleTransform(1.75f, 0.5f);
//Rotate
g.RotateTransform(45.0f,
MatrixOrder.Append);
//Fill rectangle again
g.FillRectangle(brush, rect);
//Dispose of objects
brush.Dispose();
g.Dispose();
}
}
}

FIGURE 10.34: Translate -> Rotate -> Scale composite transformation with Append
Figure 10.34 shows the output from Listing 10.23. The original rectangle is in the same place, but the transformed rectangle has moved.
Now let's keep the code from Listing 10.23 and change only the matrix transformation order from Append to Prepend, as shown in Listing 10.24.
LISTING 10.24: Translate -> Rotate -> Scale transformation order with Prepend
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Drawing.Drawing2D;
using System.Text;
using System.Windows.Forms;
namespace Text_Transformation
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void Form1_Paint(object sender, PaintEventArgs e)
{
//Create a Graphics object
Graphics g = this.CreateGraphics();
g.Clear(this.BackColor);
//Create a rectangle
Rectangle rect =
new Rectangle(20, 20, 100, 100);
//Create a solid brush
SolidBrush brush =
new SolidBrush(Color.Red);
//Fill Rectangle
g.FillRectangle(brush, rect);
//Translate
g.TranslateTransform(100.0f, 50.0f,
MatrixOrder.Prepend);
//Rotate
g.RotateTransform(45.0f,
MatrixOrder.Prepend);
//Scale
g.ScaleTransform(1.75f, 0.5f);
//Fill rectangle again
g.FillRectangle(brush, rect);
//Dispose of objects
brush.Dispose();
g.Dispose();
}
}
}
The new output is shown in figure 10.35. The matrix order affects the result.

FIGURE 10.35: Translate -> Rotate -> Scale composite transformation with Prepend
Conclusion
Hope the article would have helped you in understanding Text Transformation in GDI+. Read other articles on GDI+ on the website.
 |
This book teaches .NET developers how to work with GDI+ as they develop applications that include graphics, or that interact with monitors or printers. It begins by explaining the difference between GDI and GDI+, and covering the basic concepts of graphics programming in Windows. |