Statistics: Introduction

Introduction

In the previous chapter, we studied Python Tensorflow, its functions, and its python implementations.

In this chapter, we will start with some basics of statistics. Statistics play a very important role in machine learning, as they are used in calculating the error and the learning rate. We will discuss the error and learning rate in the coming chapters.

Data

Data is an essential part of our day to day lives. We generate millions of data according to our daily needs. This data generated is highly useful to draw conclusions and make analysis out of it.

But the question that arises in our mind is, "how"? To answer this, we use statistics.

Statistics is a branch of mathematics that deals with the process of collecting data and organizing it in a systematic manner, analyzing it, interpreting the insights and presenting it in a meaningful manner. It is the complete process of data collection to present the final outcome out of data. But the question still remains the same...

Before getting into the details, we will first deal with the question 'What is statistics?', its type, and classification.

What is Statistics?

As defined above, statistics is none other than a systematic study of data to make it into useful data which can be used to draw results and conclusion for further data analysis. Statistics is a very essential tool for data analysis.

The data we collect is classified into two categories,

Based on measurement (discrete, continuous)
Based on observation (quantitative, qualitative)

A quantitative variable is one that can be measured with the help of a standard scale, while a qualitative variable is one that cannot be measured with a standardized scale.

The variable which occurs by chance without any prediction is called a random variable. The variable which can only take fixed value is called a discrete variable.

A population can be defined as a group of values or variables. A part of a statistical population is called a sample. When we talk about the level of measurements, there are four levels of measurements, Scale 1 (Nominal scale), Scale 2 (Ordinal scale), Scale 3 (Internal), Scale 4 (Ratio).

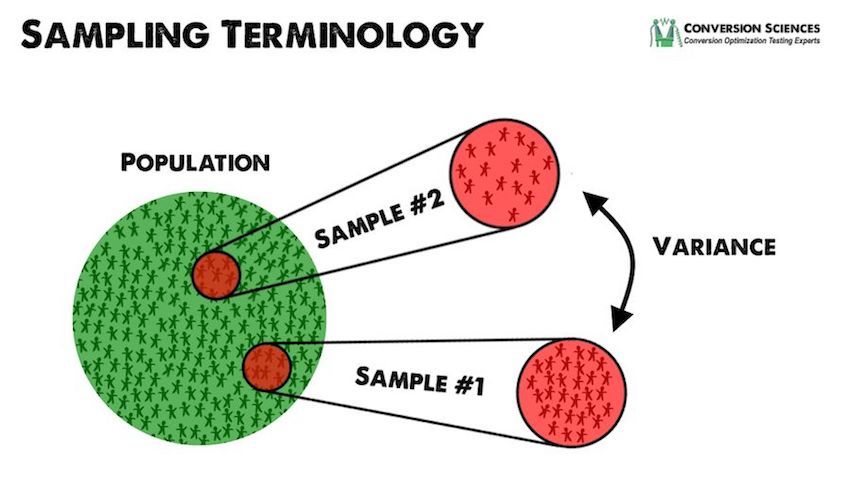
Data comes in many formats to us, which can be classified as time-series data and cross-sectional data

Time Series Data

This is a type of data consisting of observation of a single subject at different or multiple intervals of time. It primarily focuses on the same variable over a period of time. It is used to examine change within an individual over different times. It is majorly used to provide development analysis.

Cross-Sectional Data

It is a type of data consisting of observation of many subjects at a similar point in time. It primarily focuses on several variables at the same point in time. It examines the change between participants of different ages at the same time. It is used to provide information on age-related changes.

We have briefly discussed data. Now let's talk about the classification of statistics.

Statistics are briefly classified into two major categories, descriptive and inferential: