Machine Learning: Support Vector Machine

Introduction

 
In the previous chapter, we studied the k-nearest neighbors. 
 
In this chapter, we will learn support vector machine.
 
Note: ifyou can correlate anything with yourself or your life, there are greater chances of understanding the concept. So try to understand everything by relating it to humans.
 

What is Support Vector Machine?

 
Support vector machines (SVMs, also supporting vector networks) in machine learning are supervised learning models with associated learning algorithms that analyze data used for classification and regression analysis. Provided a set of training instances, each classified as belonging to one or the other of two groups, a training algorithm SVM generates a template that sells new cases for one or the other group, which renders it a non-probabilistic linear binary classifier.
 
A model from SVM describes the examples as points in space and is distributed to separate the examples of the different groups through a very broad void. There are then projected new instances in the same area and a range dependent on the portion of the distance in which they fall is predicted.
 
A hyperplane or a number of hyperplanes in a small or infinite space may be created by the support- computer and can be used for the graduation or reversal or other tasks such as the identification of outliers. The hyperplanes with the largest distance from the closest training data point of any class (so-called functional margin) intuitively achieve a good separation, as the wider the margin, the lower the generalization error of the classification system. 
 
Note:
 
When data are unlisted, supervised education is not available and there is a need for an unsupervised learning approach that attempts to find a natural grouping of data and then map new data to the groups that are formed.
 

Key Terms 

  1. Kernel
     

    • A kernel refers to a feature that converts the data into a wide space for solving the problem.
    • A linear or non-linear kernel function may be used. Kernel methods are a type of pattern analysis algorithm.
    • The kernel's primary role is to accept data as input and convert it into the appropriate output types.
    • In statistics, the mapping feature "core" measures the values of a two-dominal data in a three-dimensional spatial format and describes them. 
       

  2. Regularization
     

    • The regularization function is also named the C function in the sklearn library of python, which guides the help vector machine to optimally define each training date it wants to prevent.
    • Such a supporting vector machine example will auto-optimization if large numbers of the C parameter are used if all training data points are correctly segregated and classification is collected the hyperplanes margin that is smaller.
    • To order to obtain very tiny numbers, the algorithm can often consider that the hyperplane is a larger range and certain data points may be misclassified by the hyperplane.
       

  3. Gamma
     

    • This tuning function reiterates the length of the effect of a single data display. The low values are 'far' and the higher values are 'near' to the aircraft.
    • In measurement for a separation line, the data points with low gamma are called and are far from the possible hyper-plane separation line.
    • In comparison, the high range is used in the measurement of the hyper-plane separation line which applies to the points that are similar to the expected hyper-plane line.
       

  4. Margin
     

    • The gap is last but not least. It's also a significant tuning parameter & an integral function of a vector holder classification system.
    • The margin is the division of the line closest to the data points of the segment. In a support vector algorithm, it is necessary to have a good and proper margin. When the difference between the two data groups is greater, a strong gap is called.
    • To a strong range, the corresponding data points stay in class and thus do not move over to another level.
    • Also, the class data points will have a reasonable margin preferably at the same distance from either side of the separator panel.
       

  5. Hyperplane
     

    • A hyperplane is a linear, n-1 dimensional subset of this space, whichsplits the space into two divided parts in an n-dimensional Euclidean space.
    • For two dimensions the hyperplane is a separating line.
    • For three dimensions a plane with two dimensions divides the 3d space into two parts and thus acts as a hyperplane.
    • Thus for a space of n dimensions, we have a hyperplane of n-1 dimensions separating it into two parts.

Types of SVM

  1. Classification SVM type 1 (also known as C-SVM classification)
  2. Classification SVM type 2 (also known as nu-SVM classification)
  3. Regression SVM type 1 (also known as epsilon-SVM regression)
  4. Regression SVM type 2 (also known as nu-SVM regression)

Types of kernels

  1. Linear kernel
  2. Polynomial kernel
  3. Radial basis function kernel (RBF)/ Gaussian Kernel
  4. Sigmoid Kernel
  5. Nonlinear Kernel

Real-World Applications of SVM

  1. Face detection
     
    SVM classifies parts of the image as a face and non-face and creates a square boundary around the face.
     
  2. Text and hypertext categorization
     
    SVMs allow Text and hypertext categorization for both inductive and transductive models. They use training data to classify documents into different categories. It categorizes on the basis of the score generated and then compares with the threshold value.
     
  3. Classification of images
     
    Use of SVMs provides better search accuracy for image classification. It provides better accuracy in comparison to the traditional query-based searching techniques.
     
  4. Bioinformatics
     
    It includes protein classification and cancer classification. We use SVM for identifying the classification of genes, patients on the basis of genes, and other biological problems.
     
  5. Protein fold and remote homology detection
     
    Apply SVM algorithms for protein remote homology detection.
     
  6. Handwriting recognition
     
    We use SVMs to recognize handwritten characters used widely.
     
  7. Generalized predictive control(GPC)
     
    Use SVM based GPC to control chaotic dynamics with useful parameters.

SVM using Example

 
Like in other ML algorithms we find the best fit, in SVM we try to find a hyperplane with the maximum margin or distance, hence it is also a type of "maximum-margin" classification.
 
Let us try to understand SVM with the help of a mathematical example, for this example, 
 
Data Points Class
(-2, 4)  -1 
(4,1) -1
(1,6) 1
(2,4) 1
(6,2) 1
 
Now before I go on further I want you to first know:
 

1. Hinge loss

 
In machine learning, the hinge loss is a loss function used for training classifiers. The hinge loss is used for "maximum-margin" classification, most notably for support vector machines (SVMs).
 
The equation is given as:
 
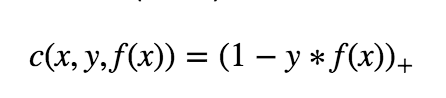
hinge1
 
where c is the loss function, x the sample, y is the true label, f(x) the predicted label.
 
You see a plus at the end, it means that the hinge error can never be negative, mathematically I can be expressed as:
 
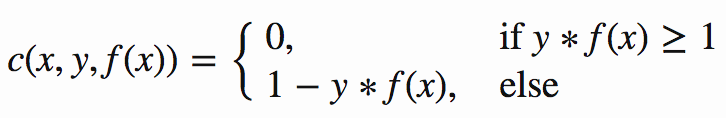
hinge2

2. Regularizer

 
The regularizer balances between margin maximization and loss. The regularizer controls the trade-off between achieving a low training error and a low testing error that is the ability to generalize your classifier to unseen data. As a regularizing parameter we choose 1/epochs, so this parameter will decrease, as the number of epochs increases.
 
Regularixer, λ = 1/epoch
 

3. Weight Vector

 
The SVM algorithm chooses a particular weight vector, that which gives rise to the “maximum margin” of separation
 
Now coming back to the math of SVM, generation of the hyperplane we can have 2 scenarios
1. Misclassification, i.e. the point is not classified correctly
2. Correct Classification
 
In the case of misclassification, we use the following to update the weights:
 
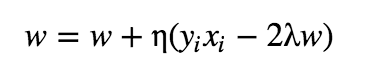
hinge3
 
and in case of correct classification, we use the following to update the weights:
 
hinge4
 
where,
  • η is the learning rate
  • λ is the regularizer
After doing the calculations, I came up with the following prediction function:
f(x) = (x, (1.56, 3.17))- 11.12
i.e f(x) = 1.56*x + 3.17*y -11.12
 
where,
  • (1.56, 3.17) is the weight vector
  • 11.12 is the bias term
Note: I will not be going into depth on how I got this, you can do the calculations by yourself or you can use sklearn to do it for you.
 
Now let us check the accuracy of the prediction function so calculated
 
1. -2*1.56 + 4*3.17 - 11.12
= -1.56
taking the sign out, we get -1, which is the correct class
 
2. 4*1.56 + 1*3.17 - 11.12
= -1.72
taking the sign out, we get -1, which is the correct class
 
3. 1*1.56 + 6*3.17 - 11.12
= 9.46
taking the sign out, we get +1, which is the correct class
 
4. 2*1.56 + 4*3.17 - 11.12
= 4.68
taking the sign out, we get +1, which is the correct class
 
5. 6*1.56 + 2*3.17 - 11.12
= 4.58
taking the sign out, we get +1, which is the correct class
 
So until now, we tested the hyperplane equation on the training data. Now its time to give some never seen before data to the model
 
Test Data = (3, 5), (-2, 3)
 
1. 3*1.56 + 5*3.17 - 11.12
= 9.41
Taking the sign out, we get +1, which is the correct class
 
2. -2*1.56 + 3*3.17 - 11.12
= -4.73
Taking the sign out, we get -1, which is the correct class
 

Python Implementation of SVM

 

1. Using Functions

 
Let us now take a look at how can we implement SVM from scratch. In the following example, we will take dummy data. I have taken the code reference from the repository.
  1. # importing some basic libraries  
  2. %matplotlib inline  
  3. import matplotlib.pyplot as plt  
  4. from matplotlib import style  
  5. style.use('ggplot')  
  6. import numpy as np  
  7.   
  8. class SVM(object):  
  9.     def __init__(self,visualization=True):  
  10.         self.visualization = visualization  
  11.         self.colors = {1:'r',-1:'b'}  
  12.         if self.visualization:  
  13.             self.fig = plt.figure()  
  14.             self.ax = self.fig.add_subplot(1,1,1)  
  15.       
  16.     def fit(self,data):  
  17.         #train with data  
  18.         self.data = data  
  19.         # { |\w\|:{w,b}}  
  20.         opt_dict = {}  
  21.           
  22.         transforms = [[1,1],[-1,1],[-1,-1],[1,-1]]  
  23.           
  24.         all_data = np.array([])  
  25.         for yi in self.data:  
  26.             all_data = np.append(all_data,self.data[yi])  
  27.                       
  28.         self.max_feature_value = max(all_data)           
  29.         self.min_feature_value = min(all_data)  
  30.         all_data = None  
  31.           
  32.         #with smaller steps our margins and db will be more precise  
  33.         step_sizes = [self.max_feature_value * 0.1,  
  34.                       self.max_feature_value * 0.01,  
  35.                       #point of expense  
  36.                       self.max_feature_value * 0.001,]  
  37.           
  38.         #extremly expensise  
  39.         b_range_multiple = 5  
  40.         #we dont need to take as small step as w  
  41.         b_multiple = 5  
  42.           
  43.         latest_optimum = self.max_feature_value*10  
  44.           
  45.         """ 
  46.         objective is to satisfy yi(x.w)+b>=1 for all training dataset such that ||w|| is minimum 
  47.         for this we will start with random w, and try to satisfy it with making b bigger and bigger 
  48.         """  
  49.         #making step smaller and smaller to get precise value  
  50.         for step in step_sizes:  
  51.             w = np.array([latest_optimum,latest_optimum])  
  52.               
  53.             #we can do this because convex  
  54.             optimized = False  
  55.             while not optimized:  
  56.                 for b in np.arange(-1*self.max_feature_value*b_range_multiple,  
  57.                                    self.max_feature_value*b_range_multiple,  
  58.                                    step*b_multiple):  
  59.                     for transformation in transforms:  
  60.                         w_t = w*transformation  
  61.                         found_option = True  
  62.                           
  63.                         #weakest link in SVM fundamentally  
  64.                         #SMO attempts to fix this a bit  
  65.                         # ti(xi.w+b) >=1  
  66.                         for i in self.data:  
  67.                             for xi in self.data[i]:  
  68.                                 yi=i  
  69.                                 if not yi*(np.dot(w_t,xi)+b)>=1:  
  70.                                     found_option=False  
  71.                         if found_option:  
  72.                             """ 
  73.                             all points in dataset satisfy y(w.x)+b>=1 for this cuurent w_t, b 
  74.                             then put w,b in dict with ||w|| as key 
  75.                             """  
  76.                             opt_dict[np.linalg.norm(w_t)]=[w_t,b]  
  77.                   
  78.                 #after w[0] or w[1]<0 then values of w starts repeating itself because of transformation  
  79.                 #Think about it, it is easy  
  80.                 #print(w,len(opt_dict)) Try printing to understand  
  81.                 if w[0]<0:  
  82.                     optimized=True  
  83.                     print("optimized a step")  
  84.                 else:  
  85.                     w = w-step  
  86.                       
  87.             # sorting ||w|| to put the smallest ||w|| at poition 0   
  88.             norms = sorted([n for n in opt_dict])  
  89.             #optimal values of w,b  
  90.             opt_choice = opt_dict[norms[0]]  
  91.   
  92.             self.w=opt_choice[0]  
  93.             self.b=opt_choice[1]  
  94.               
  95.             #start with new latest_optimum (initial values for w)  
  96.             latest_optimum = opt_choice[0][0]+step*2  
  97.       
  98.     def predict(self,features):  
  99.         #sign(x.w+b)  
  100.         classification = np.sign(np.dot(np.array(features),self.w)+self.b)  
  101.         if classification!=0 and self.visualization:  
  102.             self.ax.scatter(features[0],features[1],s=200,marker='*',c=self.colors[classification])  
  103.         return (classification,np.dot(np.array(features),self.w)+self.b)  
  104.       
  105.     def visualize(self):  
  106.         [[self.ax.scatter(x[0],x[1],s=100,c=self.colors[i]) for x in data_dict[i]] for i in data_dict]  
  107.           
  108.         # hyperplane = x.w+b (actually its a line)  
  109.         # v = x0.w0+x1.w1+b -> x1 = (v-w[0].x[0]-b)/w1  
  110.         #psv = 1     psv line ->  x.w+b = 1a small value of b we will increase it later  
  111.         #nsv = -1    nsv line ->  x.w+b = -1  
  112.         # dec = 0    db line  ->  x.w+b = 0  
  113.         def hyperplane(x,w,b,v):  
  114.             #returns a x2 value on line when given x1  
  115.             return (-w[0]*x-b+v)/w[1]  
  116.          
  117.         hyp_x_min= self.min_feature_value*0.9  
  118.         hyp_x_max = self.max_feature_value*1.1  
  119.           
  120.         # (w.x+b)=1  
  121.         # positive support vector hyperplane  
  122.         pav1 = hyperplane(hyp_x_min,self.w,self.b,1)  
  123.         pav2 = hyperplane(hyp_x_max,self.w,self.b,1)  
  124.         self.ax.plot([hyp_x_min,hyp_x_max],[pav1,pav2],'k')  
  125.           
  126.         # (w.x+b)=-1  
  127.         # negative support vector hyperplane  
  128.         nav1 = hyperplane(hyp_x_min,self.w,self.b,-1)  
  129.         nav2 = hyperplane(hyp_x_max,self.w,self.b,-1)  
  130.         self.ax.plot([hyp_x_min,hyp_x_max],[nav1,nav2],'k')  
  131.           
  132.         # (w.x+b)=0  
  133.         # db support vector hyperplane  
  134.         db1 = hyperplane(hyp_x_min,self.w,self.b,0)  
  135.         db2 = hyperplane(hyp_x_max,self.w,self.b,0)  
  136.         self.ax.plot([hyp_x_min,hyp_x_max],[db1,db2],'y--')  
  137.   
  138. #defining a basic data  
  139. data_dict = {-1:np.array([[1,7],[2,8],[3,8]]),1:np.array([[5,1],[6,-1],[7,3]])}  
  140.   
  141. svm = SVM() # Linear Kernel  
  142. svm.fit(data=data_dict)  
  143. svm.visualize()  
OUTPUT
 
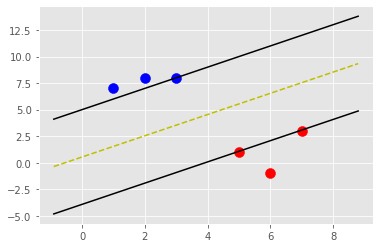
svm_scratch
  1. svm.predict([3,8])   
OUTPUT
 
(-1.0, -1.000000000000098) 
 

2. Using Sklearn

 
Let us now take a look at how can we implement SVM using sklearn. In the following example, I have used Social Network data, please find it attached. I have taken the code reference from the repository.
  1. # Importing the libraries    
  2.   
  3. import numpy as np    
  4. import matplotlib.pyplot as plt    
  5. import pandas as pd    
  6.   
  7. # Importing the datasets    
  8.   
  9. datasets = pd.read_csv('Social_Network_Ads.csv')    
  10. X = datasets.iloc[:, [2,3]].values    
  11. Y = datasets.iloc[:, 4].values    
  12.   
  13. # Splitting the dataset into the Training set and Test set    
  14.   
  15. from sklearn.model_selection import train_test_split    
  16. X_Train, X_Test, Y_Train, Y_Test = train_test_split(X, Y, test_size = 0.25, random_state = 0)    
  17.   
  18. # Feature Scaling    
  19.   
  20. from sklearn.preprocessing import StandardScaler    
  21. sc_X = StandardScaler()    
  22. X_Train = sc_X.fit_transform(X_Train)    
  23. X_Test = sc_X.transform(X_Test)    
  24.   
  25. # Fitting the classifier into the Training set    
  26.   
  27. from sklearn.svm import SVC    
  28. classifier = SVC(kernel = 'linear', random_state = 0)    
  29. classifier.fit(X_Train, Y_Train)    
  30.   
  31. # Predicting the test set results    
  32.   
  33. Y_Pred = classifier.predict(X_Test)    
  34.   
  35. # Making the Confusion Matrix     
  36.   
  37. from sklearn.metrics import confusion_matrix    
  38. cm = confusion_matrix(Y_Test, Y_Pred)    
  39.   
  40. # Visualising the Training set results    
  41.   
  42. from matplotlib.colors import ListedColormap    
  43. X_Set, Y_Set = X_Train, Y_Train    
  44. X1, X2 = np.meshgrid(np.arange(start = X_Set[:, 0].min() - 1, stop = X_Set[:, 0].max() + 1, step = 0.01),    
  45.                      np.arange(start = X_Set[:, 1].min() - 1, stop = X_Set[:, 1].max() + 1, step = 0.01))    
  46. plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),    
  47.              alpha = 0.75, cmap = ListedColormap(('red', 'green')))    
  48. plt.xlim(X1.min(), X1.max())    
  49. plt.ylim(X2.min(), X2.max())    
  50. for i, j in enumerate(np.unique(Y_Set)):    
  51.     plt.scatter(X_Set[Y_Set == j, 0], X_Set[Y_Set == j, 1],    
  52.                 c = ListedColormap(('red', 'green'))(i), label = j)    
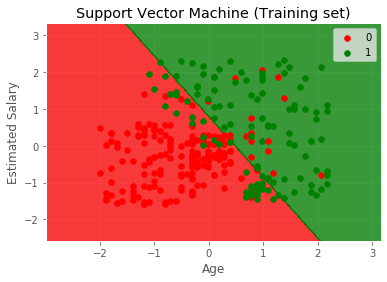
  53. plt.title('Support Vector Machine (Training set)')    
  54. plt.xlabel('Age')    
  55. plt.ylabel('Estimated Salary')    
  56. plt.legend()    
  57. plt.show()    
  58.   
  59. # Visualising the Test set results    
  60.   
  61. from matplotlib.colors import ListedColormap    
  62. X_Set, Y_Set = X_Test, Y_Test    
  63. X1, X2 = np.meshgrid(np.arange(start = X_Set[:, 0].min() - 1, stop = X_Set[:, 0].max() + 1, step = 0.01),    
  64.                      np.arange(start = X_Set[:, 1].min() - 1, stop = X_Set[:, 1].max() + 1, step = 0.01))    
  65. plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),    
  66.              alpha = 0.75, cmap = ListedColormap(('red', 'green')))    
  67. plt.xlim(X1.min(), X1.max())    
  68. plt.ylim(X2.min(), X2.max())    
  69. for i, j in enumerate(np.unique(Y_Set)):    
  70.     plt.scatter(X_Set[Y_Set == j, 0], X_Set[Y_Set == j, 1],    
  71.                 c = ListedColormap(('red', 'green'))(i), label = j)    
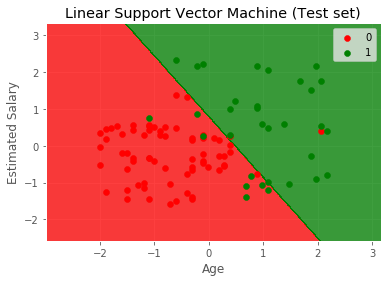
  72. plt.title('Linear Support Vector Machine (Test set)')    
  73. plt.xlabel('Age')    
  74. plt.ylabel('Estimated Salary')    
  75. plt.legend()    
  76. plt.show()     
  77.   
  78. from sklearn.svm import SVC      
  79. classifier = SVC(kernel = 'rbf', random_state = 0)      
  80. classifier.fit(X_Train, Y_Train)      
  81.   
  82. # Predicting the test set results      
  83.   
  84. Y_Pred = classifier.predict(X_Test)      
  85.   
  86. # Making the Confusion Matrix       
  87.   
  88. from sklearn.metrics import confusion_matrix      
  89. cm = confusion_matrix(Y_Test, Y_Pred)           
  90.   
  91. # Visualising the Test set results      
  92.   
  93. from matplotlib.colors import ListedColormap      
  94. X_Set, Y_Set = X_Test, Y_Test      
  95. X1, X2 = np.meshgrid(np.arange(start = X_Set[:, 0].min() - 1, stop = X_Set[:, 0].max() + 1, step = 0.01),      
  96.                      np.arange(start = X_Set[:, 1].min() - 1, stop = X_Set[:, 1].max() + 1, step = 0.01))      
  97. plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),      
  98.              alpha = 0.75, cmap = ListedColormap(('red', 'green')))      
  99. plt.xlim(X1.min(), X1.max())      
  100. plt.ylim(X2.min(), X2.max())      
  101. for i, j in enumerate(np.unique(Y_Set)):      
  102.     plt.scatter(X_Set[Y_Set == j, 0], X_Set[Y_Set == j, 1],      
  103.                 c = ListedColormap(('red', 'green'))(i), label = j)      
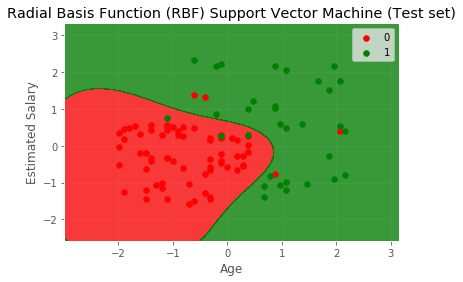
  104. plt.title('Radial Basis Function (RBF) Support Vector Machine (Test set)')      
  105. plt.xlabel('Age')      
  106. plt.ylabel('Estimated Salary')      
  107. plt.legend()      
  108. plt.show()     
OUTPUT
svm_input
 
svm_linear_output
 
svm_rbf_output
 

3. Using Tensorflow

 
Let us now take a look at how can we implement SVM using TensorFlow. In the following example, I am using the IRIS dataset. I have taken the code reference from the repository.
 
Note: tf.disable_v2_behaviour() is used to use the Tensorflow 1 functionalities, as i have Tensorflow 2 installed on my PC.
  1. import matplotlib.pyplot as plt    
  2. import numpy as np    
  3. import tensorflow.compat.v1 as tf    
  4. tf.disable_v2_behavior()    
  5. from sklearn import datasets    
  6. from tensorflow.python.framework import ops    
  7. ops.reset_default_graph()    
  8.   
  9. # Set random seeds    
  10. np.random.seed(7)    
  11. tf.set_random_seed(7)    
  12.   
  13. # Create graph    
  14. sess = tf.Session()    
  15.   
  16. # Load the data    
  17. # iris.data = [(Sepal Length, Sepal Width, Petal Length, Petal Width)]    
  18. iris = datasets.load_iris()    
  19. x_vals = np.array([[x[0], x[3]] for x in iris.data])    
  20. y_vals = np.array([1 if y == 0 else -1 for y in iris.target])    
  21.   
  22. # Split data into train/test sets    
  23. train_indices = np.random.choice(len(x_vals),    
  24.                                  int(round(len(x_vals)*0.9)),    
  25.                                  replace=False)    
  26. test_indices = np.array(list(set(range(len(x_vals))) - set(train_indices)))    
  27. x_vals_train = x_vals[train_indices]    
  28. x_vals_test = x_vals[test_indices]    
  29. y_vals_train = y_vals[train_indices]    
  30. y_vals_test = y_vals[test_indices]    
  31.   
  32. # Declare batch size    
  33. batch_size = 135    
  34.   
  35. # Initialize placeholders    
  36. x_data = tf.placeholder(shape=[None, 2], dtype=tf.float32)    
  37. y_target = tf.placeholder(shape=[None, 1], dtype=tf.float32)    
  38.   
  39. # Create variables for linear regression    
  40. A = tf.Variable(tf.random_normal(shape=[2, 1]))    
  41. b = tf.Variable(tf.random_normal(shape=[1, 1]))    
  42.   
  43. # Declare model operations    
  44. model_output = tf.subtract(tf.matmul(x_data, A), b)    
  45.   
  46. # Declare vector L2 'norm' function squared    
  47. l2_norm = tf.reduce_sum(tf.square(A))    
  48.   
  49. # Declare loss function    
  50. # Loss = max(0, 1-pred*actual) + alpha * L2_norm(A)^2    
  51. # L2 regularization parameter, alpha    
  52. alpha = tf.constant([0.01])    
  53. # Margin term in loss    
  54. classification_term = tf.reduce_mean(tf.maximum(0., tf.subtract(1., tf.multiply(model_output, y_target))))    
  55. # Put terms together    
  56. loss = tf.add(classification_term, tf.multiply(alpha, l2_norm))    
  57.   
  58. # Declare prediction function    
  59. prediction = tf.sign(model_output)    
  60. accuracy = tf.reduce_mean(tf.cast(tf.equal(prediction, y_target), tf.float32))    
  61.   
  62. # Declare optimizer    
  63. my_opt = tf.train.GradientDescentOptimizer(0.01)    
  64. train_step = my_opt.minimize(loss)    
  65.   
  66. # Initialize variables    
  67. init = tf.global_variables_initializer()    
  68. sess.run(init)    
  69.   
  70. # Training loop    
  71. loss_vec = []    
  72. train_accuracy = []    
  73. test_accuracy = []    
  74. for i in range(500):    
  75.     rand_index = np.random.choice(len(x_vals_train), size=batch_size)    
  76.     rand_x = x_vals_train[rand_index]    
  77.     rand_y = np.transpose([y_vals_train[rand_index]])    
  78.     sess.run(train_step, feed_dict={x_data: rand_x, y_target: rand_y})    
  79.   
  80.     temp_loss = sess.run(loss, feed_dict={x_data: rand_x, y_target: rand_y})    
  81.     loss_vec.append(temp_loss)    
  82.   
  83.     train_acc_temp = sess.run(accuracy, feed_dict={    
  84.         x_data: x_vals_train,    
  85.         y_target: np.transpose([y_vals_train])})    
  86.     train_accuracy.append(train_acc_temp)    
  87.   
  88.     test_acc_temp = sess.run(accuracy, feed_dict={    
  89.         x_data: x_vals_test,    
  90.         y_target: np.transpose([y_vals_test])})    
  91.     test_accuracy.append(test_acc_temp)    
  92.   
  93.     if (i + 1) % 100 == 0:    
  94.         print('Step #{} A = {}, b = {}'.format(    
  95.             str(i+1),    
  96.             str(sess.run(A)),    
  97.             str(sess.run(b))    
  98.         ))    
  99.         print('Loss = ' + str(temp_loss))    
  100.   
  101. # Extract coefficients    
  102. [[a1], [a2]] = sess.run(A)    
  103. [[b]] = sess.run(b)    
  104. slope = -a2/a1    
  105. y_intercept = b/a1    
  106.   
  107. # Extract x1 and x2 vals    
  108. x1_vals = [d[1] for d in x_vals]    
  109.   
  110. # Get best fit line    
  111. best_fit = []    
  112. for i in x1_vals:    
  113.     best_fit.append(slope*i+y_intercept)    
  114.   
  115. # Separate I. setosa    
  116. setosa_x = [d[1] for i, d in enumerate(x_vals) if y_vals[i] == 1]    
  117. setosa_y = [d[0] for i, d in enumerate(x_vals) if y_vals[i] == 1]    
  118. not_setosa_x = [d[1] for i, d in enumerate(x_vals) if y_vals[i] == -1]    
  119. not_setosa_y = [d[0] for i, d in enumerate(x_vals) if y_vals[i] == -1]    
  120.   
  121. # Plot data and line    
  122. plt.plot(setosa_x, setosa_y, 'o', label='I. setosa')    
  123. plt.plot(not_setosa_x, not_setosa_y, 'x', label='Non-setosa')    
  124. plt.plot(x1_vals, best_fit, 'r-', label='Linear Separator', linewidth=3)    
  125. plt.ylim([0, 10])    
  126. plt.legend(loc='lower right')    
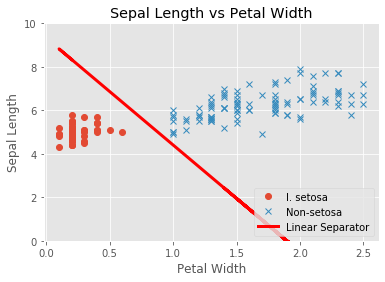
  127. plt.title('Sepal Length vs Petal Width')    
  128. plt.xlabel('Petal Width')    
  129. plt.ylabel('Sepal Length')    
  130. plt.show()    
  131.   
  132. # Plot train/test accuracies    
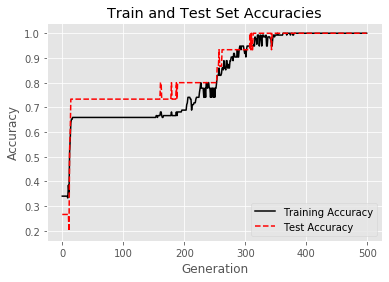
  133. plt.plot(train_accuracy, 'k-', label='Training Accuracy')    
  134. plt.plot(test_accuracy, 'r--', label='Test Accuracy')    
  135. plt.title('Train and Test Set Accuracies')    
  136. plt.xlabel('Generation')    
  137. plt.ylabel('Accuracy')    
  138. plt.legend(loc='lower right')    
  139. plt.show()    
  140.   
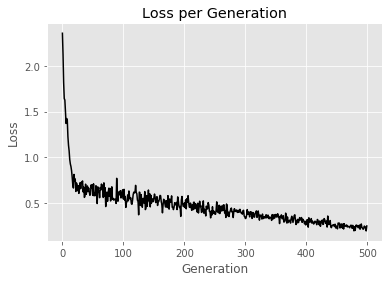
  141. # Plot loss over time    
  142. plt.plot(loss_vec, 'k-')    
  143. plt.title('Loss per Generation')    
  144. plt.xlabel('Generation')    
  145. plt.ylabel('Loss')    
  146. plt.show()   
OUTPUT
 
Step #100 A = [[-0.4810509 ][ 0.05859518]], b = [[-1.8697345]]Loss = [0.64420575]
Step #200 A = [[-0.4076391 ][-0.25413615]], b = [[-1.9181045]]Loss = [0.45963168]
Step #300 A = [[-0.34309638][-0.55148035]], b = [[-1.9694378]]Loss = [0.34777495]
Step #400 A = [[-0.28505743][-0.83066034]], b = [[-2.023808]]Loss = [0.25850892]
Step #500 A = [[-0.22314341][-1.096483 ]], b = [[-2.0792139]]Loss = [0.2473848]
 
tensorflow_input
 
svm_train_test_tensorflow
 
svm_loss_tensorflow

Conclusion

 
In this chapter, we studied the support vector machine.
 
With this, we are done with learning machine learning algorithms. Now its time to do some hands-on. So from the next chapter onwards, we will do some projects.
Author
Rohit Gupta
65 27.3k 3m
Next » Machine Leaning Project 1: Housing Price Prediction

©2024 C# Corner.