Machine Learning: Naive Bayes
Introduction
In the previous chapter, we studied Decision Tree.
In this chapter, we will study naive bayes.
Key Terms
1. Coin
A coin has two sides, Head and
Tail. If an event consists of more than one coin, then coins are considered as distinct, if not otherwise stated.
2. Die
The die has six faces marked 11, 2, 3, 4, 5, and 6. If we have more than one
dice, then all dice are considered as distinct, if not otherwise
stated.3. Playing Cards
A pack of playing cards
has 52 cards. There are 4 suits (spade, heart, diamond, and club) each having 13 cards. There are two colors, red (heart and diamond) and black
(spade and club) each having 26 cards.
In 13 cards of each suit,
there are 3 face cards namely king, queen and jack so there are in all
’12 face cards. Also, there are 16 honor cards,
4 of each suit namely ace, king, queen, and jack.
Types of Experiments
2. Probabilistic/Random Experiment
Those
experiments, which when repeated under identical conditions, do not
produce the same outcome every time but the outcome in a trial is one of
the several possible outcomes called a random experiment.
Important Definitions
Let a random experiment, be repeated under identical conditions, then the experiment is called a Trial.
(ii)
Sample Space
The set of all possible outcomes of an experiment is called the sample space of the experiment and it is denoted by S.
(iii) Event
A subset of the sample space associated with a random experiment is called an event or case.
(iv) Sample Points
The outcomes of an experiment are called the sample point.
(v) Certain Event
An event that must occur, whatever be the outcomes, is called a certain or sure event.
(vi) Impossible Event
An event that cannot occur in a particular random experiment is called an impossible event.
(vii) Elementary Event
An event certainly only one sample point is called elementary event or indecomposable events.
(viii)
Favorable Event
Let S be the sample space associated with a random experiment and let E ⊂ S. Then, the elementary events belonging to E are known as the favorable event to E.
(ix) Compound Events
An event certainly more than one sample point is called compound events or decomposable events.
Probability
Types of Events
The given events are said to be equally likely if none of them is expected to occur in preference to the other.
(ii)
Mutually Exclusive Events
A set of events is said to be mutually
exclusive if the happening of one excludes the happening of the other.
If A and B are mutually exclusive, then P(A ∩ B) = 0
(iii)
Exhaustive Events
A set of events is said to be exhaustive if the
performance of the experiment always results in the occurrence of at least one of them.
If E1, E2, … , En are exhaustive events, then El ∪ E2 ∪ … ∪ En = S i.e., P(E1 ∪ E2 ∪ E3 ∪ … ∪ En) = 1
(iv)
Independent Events
Two events A and B associated with a random
experiment are independent if the probability of occurrence or
non-occurrence of A is not affected by the occurrence or non-occurrence
of B.
i.e., P(A ∩ B) = P(A) P(B)
The complement of an Event
(i) P(A ∪ A’) = S
(ii) P(A ∩ A’) = φ
(iii) P(A’)’ = A
Partition of a Sample Space
(i) Ai ∩ Aj = φ; i ≠ j; i,j= 1,2, …. ,n
(ii) A1 ∪ A2 ∪ … ∪ An = S
(iii) P(Ai) > 0, ∀ i = 1,2, …. ,n
Important Results on Probability
A1 ∩ A2 ∩ A3 ∩ …∩ An = φ
P(A1 ∪ A2 ∪ A3 ∪… ∪ An) = P(A1) + (A2) + … + P(An)
and A1 ∩ A2 ∩ A3 ∩ …∩ An = 0
(ii) If a set of events A1, A2,…., An are exhaustive, then
P(A1 ∪ A2 ∪ … ∪ An) = 1
(iii) The probability of an impossible event is O. i.e., P(A) = 0 if A is an impossible event. ,
(iv) Probability of any event in a sample space is 1. i.e., P(A) = 1
(v) Odds in favour of A = P(A) / P(A)
(vi) Odds in Against of A = P(A) / P(A)
(vii) Addition Theorem of Probability
(a) For two events A and B
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(b) For three events A, B and C
P(A ∪ B ∪ C) = P(A) + P(B) + P(C) -P(A ∩ B) – P(B ∩ C) – P(A ∩ C) + P(A ∩ B ∩ C)
(c) For n events A1, A2,…., An
(viii) If A and B are two events, then
P(A ∩ B) ≤ P(A) ≤ P(A ∪ B) ≤ P(A) + P(B)
(ix) If A and B are two events associated with a random experiment, then
(a) P(A ∩ B) = P(B) – P(A ∩ B)
(b) P(A ∩ B) = P(A) – P(A ∩ B)
(c)P [(A ∩ B) ∪ (A ∩ B)] = P(A) + P(B) – 2P(A ∩ B)
(d) P(A ∩ B) = 1- P(A ∪ B)
(e) P(A ∪ B) = 1- P(A ∩ B)
(f) P(A) = P(A ∩ B) + P(A ∩ B).
(g) P(B) = P(A ∩ B) + P(B ∩ A)
(x)
(a) P (exactly one of A, B occurs)
= P(A) + P(B) – 2P(A ∩ B) = P(A ∪ B) – P(A ∩ B)
(b) P(neither A nor B) = P(A’ ∩ B’) = 1 – P(A ∪ B)
(xi) If A, B and C are three events, then
(a) P(exactly one of A, B, C occurs)
= P(A) + P(B) + P(C) – 2P(A ∩ B) – 2P(B ∩ C) – 2P(A ∩ C) + 3P(A ∩ B ∩ C)
(b) P (at least two of A, B, C occurs)
= P(A ∩ B) + P(B ∩ C) + P(C ∩ A) – 2P(A ∩ B ∩ C)
(c) P (exactly two of A, B, C occurs) .
= P(A ∩ B) + P(B ∩ C) + P(A ∩ C) – 3P(A ∩ B ∩ C)
(xii)
(a) P(A ∪ B) = P(A) + P(B), if A and B are mutually exclusive events.
(b) P(A ∪ B ∪ C) = P(A) + P(B) + P(C), if A, Band C are mutually exclusive events.
(xiii) P(A) = 1- P(A)
(xiv) P(A ∪ B) = P(S) = 1, P(φ) = 0
(xv) P(A ∩ B) = P(A) x P(B), if A and B are independent events.
(xvi)
If A1, A2,…., An are independent events associated with a random
experiment, the probability of occurrence of at least one
= P(A1 ∪ A2 ∪…. ∪ An)
= 1 – P(A1 ∪ A2 ∪…. ∪ An)
= 1 – P(A1)P(A2)…P(An)
(xvii) If B ⊆ A, then P(A ∩ B) = P(A) – P(B)
Conditional Probability
i.e., P(A/B) = P(A ∩ B) / P(B)
If A has already occurred and P (A) ≠ 0, then
P(B/A) = P(A ∩ B) / P(A)
Also, P(A / B) + P (A / B) = 1
Multiplication Theorem on Probability
P(A ∩ B) = P(A)P(B /A), IF P(A) ≠ 0
OR
P(A ∩ B) = P(B)P(A /B), IF P(B) ≠ 0
(ii) If A1, A2,…., An are n events associated with a random experiment, then
P(A1 ∩ A2 ∩…. ∩ An) = P(A1) P(A2 / A1) P(A3 / (A1 ∩ A2)) …P(An / (A1 ∩ A2 ∩ A3 ∩…∩A n – 1))
Total Probability
P(A) = P(E1)P(A / E1) + P(E2)P(A / E2) + … + P(En) P(A / En)
Baye’s Theorem
where,
- P (Ei), i = 1,2, n are known as the prior probabilities
- P (A / Ei), i = 1,2, , n are called the likelihood probabilities
- P (Ei / A), i = 1, 2, … ,n is called the posterior probabilities
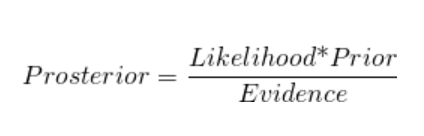
OR
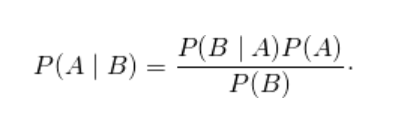
- P ( A ∣ B ) is a conditional probability: the likelihood of event A occurring given that B is true.
- P ( B ∣ A ) is also a conditional probability: the likelihood of event B occurring given that A is true.
- P ( A ) and P ( B ) are the probabilities of observing A and B independently of each other; this is known as the marginal probability.
Random Variable
X: U → R is called a random variable.
There are two types of random variables.
(i)
Discrete Random Variable
If the range of the real function X: U → R
is a finite set or an infinite set of real numbers, it is called a
discrete random variable.
(ii) Continuous Random Variable
If the
range of X is an interval (a, b) of R, then X is called a continuous
random variable. e.g., In tossing of two coins S = {HH, HT, TH, TT},
let X denotes the number of heads in the tossing of two coins, then X(HH) = 2, X(TH) = 1, X(TT) = 0
Probability Distribution
Mathematical Expectation/Mean
E(X) = X = P1X1 + P2X2 + … + PnXn = Σni = 1 PiXi
Important Results
(i) Variance V(X) = σ2x = E(X2) – (E(X))2
where, E(X2) = Σni = 1 x2iP(xi)
(ii) Standard Deviation
√V(X) = σx = √E(X2) – (E(X))2
(iii) If Y = a X + b, then
(a) E(Y) = E(aX + b) = aE(X) + b
(b) σ2y = a2V(Y) = a2σ2x
(c) σy = √V(Y) = |a|σx
(iv) If Z = aX2 + bX + c, then
E(Z) = E(aX2 + bX + c)
= aE(X2) + bE(X) + c
Baye's Theorem Explanation using an example
Let us try to understand the above formula through an example:
Question
Talking about C-SharpCorner, if a person visits C-SharpCorner, the chances of he/she revisiting are 60%, the chances of a person liking a particular article are 75%. Chances of a person liking the article and coming back are 75%. So we need to find the probability of a person re-visiting the website given that he/she doesn't like the article.
Solution
A: A person re-visits the website
B: A person likes an article
So, P(A) = 0.6, P(A') = 0.4
P(B) = 0.75 , P(B') =0.25
P(A|B) = 0.75, P(A'|B) = 0.25
P(B|A') = P((A'|B)*P(B))/ P(A')
= (0.25*0.75)/0.4
= 0.46875
So, from the above calculations, it is clear that a person will revisit ~47% time if he/she doesn't like a particular article
When is Naive Bayes Classifier Used?
1. Real-time prediction
Naive Bayes Algorithm is fast and always ready to learn hence best suited for real-time predictions.
2. Multi-class prediction
The probability of multi-classes of any target variable can be predicted using a Naive Bayes algorithm.
3. Recommendation system
Naive Bayes classifier with the help of Collaborative Filtering builds a Recommendation System. This system uses data mining and machine learning techniques to filter the information which is not seen before and then predict whether a user would appreciate a given resource or not.
4. Text classification/ Sentiment Analysis/ Spam Filtering
Due to its better performance with multi-class problems and its independence rule, Naive Bayes algorithm performs better or have a higher success rate in text classification, Therefore, it is used in Sentiment Analysis and Spam filtering.
Difference between Bayes and Naive Bayes Algorithm
The naive Bayes classifier is an approximation to the Bayes classifier, in which we assume that the features are conditionally independent given the class instead of modeling their full conditional distribution given the class.
A Bayes classifier is best interpreted as a decision rule. Suppose we seek to estimate the class of ("classify") an observation is given a vector of features. Denote the class C and the vector of features (F1, F2,…, Fk). Given a probability model underlying the data (that is, given the joint distribution of (C, F1, F2,…, Fk), the Bayes classification function chooses a class by maximizing the probability of the class given the observed features:
argmaxc P(C=c∣F1=f1,…,Fk=fk)
Assumptions of Naive Bayes Algorithm
- All the features are independent, that is there are no dependencies between any of the features.
- Each of the features is given equal or the same importance or equal weight
Things to keep in mind to get the best out of Naive Bayes Algorithm
- Categorical Inputs
Naive Bayes assumes label attributes such as binary, categorical, or nominal.
- Gaussian Inputs
If the input variables are real-valued, a Gaussian distribution is assumed. In which case the algorithm will perform better if the univariate distributions of your data are Gaussian or near-Gaussian. This may require removing outliers (e.g. values that are more than 3 or 4 standard deviations from the mean). - Classification Problems
Naive Bayes works best with binary and multiclass classification. - Log Probabilities
The calculation of the likelihood of different class values involves multiplying a lot of small numbers together. We should use a log transform of the probabilities to avoid an underflow of numerical precision. - Kernel Functions
Rather than assuming a Gaussian distribution for numerical input values, more complex distributions can be used such as a variety of kernel density functions. - Update Probabilities
When new data becomes available, you can simply update the probabilities of your model. This can be helpful if the data changes frequently.
Types of Naive Bayes Algorithm
1. Multinomial Naive Bayes
This
is mostly used for the document classification problems, i.e whether a
the document belongs to the category of sports, politics, technology, etc.
The features/predictors used by the classifier are the frequency of the
words present in the document.
2. Bernoulli Naive Bayes
This
is similar to the multinomial naive Bayes but the predictors are
boolean variables. The parameters that we use to predict the class
the variable takes up only values yes or no, for example, if a word occurs in
the text or not.
3. Gaussian Naive Bayes
When
the predictors take up a continuous value and are not discrete, we
assume that these values are sampled from a gaussian distribution.
4. Semi-supervised parameter estimation
What is Naive Bayes?
| Type | Long | Not Long | Sweet | Not Sweet | Yellow | Not Yellow | Total |
| Banana | 400 | 100 | 350 | 150 | 450 | 50 | 500 |
| Orange | 0 | 300 | 150 | 150 | 300 | 0 | 300 |
| Other | 100 | 100 | 150 | 50 | 50 | 150 | 200 |
| Total | 500 | 500 | 650 | 350 | 800 | 200 | 1000 |
So the objective of the classifier is to predict if a given fruit is a ‘Banana’ or ‘Orange’ or ‘Other’ when only the 3 features (long, sweet, and yellow) are known.
So to predict this we need to find 3 probabilities. Let's start
1. We first calculate the "Prior" probabilities for each of the class of fruits
P[Y=Banana] = 500/1000 = 0.5
P[Y=Orange] = 300/1000 = 0.3
P[Y=Other] = 200/1000 = 0.2
2. We then compute the probability of evidence that goes in the denominator
P[x1=Long] = 500/100 = 0.5
P[x2=Sweet] = 650/100 = 0.65
P[x3=Yellow] = 800/100 = 0.8
3. Now we calculate the probability of likelihood of evidences that goes in the numerator
P[x1=Long | Y=Banana] = 400/500 = 0.8
P[x2=Sweet | Y=Banana] = 350/500 = 0.7
P[x3=Yellow | Y=Banana] = 450/500 = 0.9
4. At the end we substitute all the values in the Naive Bayes Formula,
a. P(Banana | Long, Sweet and Yellow)
= ((P(Long | Banana) * P(Sweet | Banana) * P(Yellow | Banana))*P(Banana))/ (P(Long) * P(Sweet) * P(Yellow))
= ((0.8 * 0.7 * 0.9) * 0.5)/(0.5 * 0.65 * 0.8)
= 0.97
b. P(Orange | Long, Sweet and Yellow)
= ((P(Long | Orange) * P(Sweet | Orange) * P(Yellow | Orange))*P(Orange))/ (P(Long) * P(Sweet) * P(Yellow))
= 0
c. P(Others | Long, Sweet and Yellow)
= ((P(Long | Others) * P(Sweet | Others) * P(Yellow | Others))*P(Others))/ (P(Long) * P(Sweet) * P(Yellow))
= 0.07
So, from the Naive Bayes Classifier, we predict the fruit is a Banana.
Python Implementation of Decision Tree
Let's
take the example of the IRIS dataset, you can directly import it from the sklearn dataset repository. Feel free to use any dataset,
there some very good datasets available on kaggle and with Google Colab.
1. Using functions
- from csv import reader
- from math import sqrt
- from math import exp
- from math import pi
- # Load a CSV file
- def load_csv(filename):
- dataset = list()
- with open(filename, 'r') as file:
- csv_reader = reader(file)
- for row in csv_reader:
- if not row:
- continue
- dataset.append(row)
- return dataset
- # Convert string column to float
- def str_column_to_float(dataset, column):
- for row in dataset:
- row[column] = float(row[column].strip())
- # Convert string column to integer
- def str_column_to_int(dataset, column):
- class_values = [row[column] for row in dataset]
- unique = set(class_values)
- lookup = dict()
- for i, value in enumerate(unique):
- lookup[value] = i
- print('[%s] => %d' % (value, i))
- for row in dataset:
- row[column] = lookup[row[column]]
- return lookup
- # Split the dataset by class values, returns a dictionary
- def separate_by_class(dataset):
- separated = dict()
- for i in range(len(dataset)):
- vector = dataset[i]
- class_value = vector[-1]
- if (class_value not in separated):
- separated[class_value] = list()
- separated[class_value].append(vector)
- return separated
- # Calculate the mean of a list of numbers
- def mean(numbers):
- return sum(numbers)/float(len(numbers))
- # Calculate the standard deviation of a list of numbers
- def stdev(numbers):
- avg = mean(numbers)
- variance = sum([(x-avg)**2 for x in numbers]) / float(len(numbers)-1)
- return sqrt(variance)
- # Calculate the mean, stdev and count for each column in a dataset
- def summarize_dataset(dataset):
- summaries = [(mean(column), stdev(column), len(column)) for column in zip(*dataset)]
- del(summaries[-1])
- return summaries
- # Split dataset by class then calculate statistics for each row
- def summarize_by_class(dataset):
- separated = separate_by_class(dataset)
- summaries = dict()
- for class_value, rows in separated.items():
- summaries[class_value] = summarize_dataset(rows)
- return summaries
- # Calculate the Gaussian probability distribution function for x
- def calculate_probability(x, mean, stdev):
- exponent = exp(-((x-mean)**2 / (2 * stdev**2 )))
- return (1 / (sqrt(2 * pi) * stdev)) * exponent
- # Calculate the probabilities of predicting each class for a given row
- def calculate_class_probabilities(summaries, row):
- total_rows = sum([summaries[label][0][2] for label in summaries])
- probabilities = dict()
- for class_value, class_summaries in summaries.items():
- probabilities[class_value] = summaries[class_value][0][2]/float(total_rows)
- for i in range(len(class_summaries)):
- mean, stdev, _ = class_summaries[i]
- probabilities[class_value] *= calculate_probability(row[i], mean, stdev)
- return probabilities
- # Predict the class for a given row
- def predict(summaries, row):
- probabilities = calculate_class_probabilities(summaries, row)
- best_label, best_prob = None, -1
- for class_value, probability in probabilities.items():
- if best_label is None or probability > best_prob:
- best_prob = probability
- best_label = class_value
- return best_label
- # Make a prediction with Naive Bayes on Iris Dataset
- filename = 'iris.csv'
- dataset = load_csv(filename)
- for i in range(len(dataset[0])-1):
- str_column_to_float(dataset, i)
- # convert class column to integers
- str_column_to_int(dataset, len(dataset[0])-1)
- # fit model
- model = summarize_by_class(dataset)
- # define a new record
- row = [5.7,2.9,4.2,1.3]
- # predict the label
- label = predict(model, row)
- print('Data=%s, Predicted: %s' % (row, label))
[Iris-versicolor] => 0
[Iris-setosa] => 1
[Iris-virginica] => 2
Data=[5.7, 2.9, 4.2, 1.3], Predicted: 0
2. Using Sklearn
- from sklearn import datasets
- #Load dataset
- wine = datasets.load_wine()
- # print the names of the 13 features
- print ("Features: ", wine.feature_names)
-
- # print the label type of wine(class_0, class_1, class_2)
- print ("Labels: ", wine.target_names)
- # Import train_test_split function
- from sklearn.model_selection import train_test_split
- # Split the dataset into the training set and test set
- X_train, X_test, y_train, y_test = train_test_split(wine.data, wine.target, test_size=0.3,random_state=109)
- #Import Gaussian Naive Bayes model
- from sklearn.naive_bayes import GaussianNB
- #Create a Gaussian Classifier
- gnb = GaussianNB()
-
- #Train the model using the training sets
- gnb.fit(X_train, y_train)
- #Predict the response for test dataset
- y_pred = gnb.predict(X_test)
- print("y_pred: ",y_pred)
- #Import scikit-learn metrics module for accuracy calculation
- from sklearn import metrics
- # Model Accuracy, how often is the classifier correct?
- print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
The output that I got is
Features: ['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
Labels: ['class_0' 'class_1' 'class_2']
y_pred: [0 0 1 2 0 1 0 0 1 0 2 2 2 2 0 1 1 0 0 1 2 1 0 2 0 0 1 2 0 1 2 1 1 0 1 1 0 2 2 0 2 1 0 0 0 2 2 0 1 1 2 0 0 2]
Accuracy: 0.9074074074074074
3. Using TensorFlow
- from IPython import embed
- from matplotlib import colors
- from matplotlib import pyplot as plt
- from sklearn import datasets
- import numpy as np
- import tensorflow as tf
- from sklearn.utils.fixes import logsumexp
- import numpy as np
-
- class TFNaiveBayesClassifier:
- dist = None
- def fit(self, X, y):
- # Separate training points by class (nb_classes * nb_samples * nb_features)
- unique_y = np.unique(y)
- points_by_class = np.array([
- [x for x, t in zip(X, y) if t == c]
- for c in unique_y])
- # Estimate mean and variance for each class / feature
- # shape: nb_classes * nb_features
- mean, var = tf.nn.moments(tf.constant(points_by_class), axes=[1])
- # Create a 3x2 univariate normal distribution with the
- # known mean and variance
- self.dist = tf.distributions.Normal(loc=mean, scale=tf.sqrt(var))
- def predict(self, X):
- assert self.dist is not None
- nb_classes, nb_features = map(int, self.dist.scale.shape)
- # Conditional probabilities log P(x|c) with shape
- # (nb_samples, nb_classes)
- cond_probs = tf.reduce_sum(
- self.dist.log_prob(
- tf.reshape(
- tf.tile(X, [1, nb_classes]), [-1, nb_classes, nb_features])),
- axis=2)
- # uniform priors
- priors = np.log(np.array([1. / nb_classes] * nb_classes))
- # posterior log probability, log P(c) + log P(x|c)
- joint_likelihood = tf.add(priors, cond_probs)
- # normalize to get (log)-probabilities
- norm_factor = tf.reduce_logsumexp(
- joint_likelihood, axis=1, keep_dims=True)
- log_prob = joint_likelihood - norm_factor
- # exp to get the actual probabilities
- return tf.exp(log_prob)
- if __name__ == '__main__':
- iris = datasets.load_iris()
- # Only take the first two features
- X = iris.data[:, :2]
- y = iris.target
- tf_nb = TFNaiveBayesClassifier()
- tf_nb.fit(X, y)
- # Create a regular grid and classify each point
- x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
- y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
- xx, yy = np.meshgrid(np.linspace(x_min, x_max, 30),
- np.linspace(y_min, y_max, 30))
- s = tf.Session()
- Z = s.run(tf_nb.predict(np.c_[xx.ravel(), yy.ravel()]))
- # Extract probabilities of class 2 and 3
- Z1 = Z[:, 1].reshape(xx.shape)
- Z2 = Z[:, 2].reshape(xx.shape)
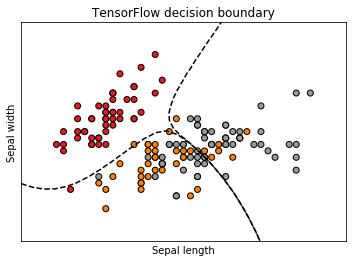
- # Plot
- fig = plt.figure(figsize=(5, 3.75))
- ax = fig.add_subplot(111)
- ax.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1,
- edgecolor='k')
- # Swap signs to make the contour dashed (MPL default)
- ax.contour(xx, yy, -Z1, [-0.5], colors='k')
- ax.contour(xx, yy, -Z2, [-0.5], colors='k')
- ax.set_xlabel('Sepal length')
- ax.set_ylabel('Sepal width')
- ax.set_title('TensorFlow decision boundary')
- ax.set_xlim(x_min, x_max)
- ax.set_ylim(y_min, y_max)
- ax.set_xticks(())
- ax.set_yticks(())
- plt.tight_layout()
- fig.savefig('tf_iris.png', bbox_inches='tight')
Conclusion
In this article, we studied naive bayes.
In the next chapter, we will study k-means clustering.
Author
Rohit Gupta
55
29.2k
3.1m
