Machine Learning: Multiple Linear Regression

Introduction

 
In the previous chapter, we studied Logistic Regression. 
 
In this chapter, we will learn Multiple Linear Regression.
 
Note: ifyou can correlate anything with yourself or your life, there are greater chances of understanding the concept. So try to understand everything by relating it to humans.
 

When we should use Multiple Linear Regression?

 
Multiple Linear Regression is an extended version of simple Linear regression, with one most important difference being the number of features it can handle. Multiple Linear Regression can handle more than 1 feature. So, we should use Multiple Linear Regression in cases where the dataset is uniformly distributed and has more than 1 feature to process. 
 

How do we calculate Multiple Linear Regression? 

 
The formula of the linear regression doesn't change, it remains y= m*X+b, only the number of coefficients increases
 
f_MLR

Multiple Linear Regression 

 
Multiple linear regression (MLR) or multiple regression, is a statistical technique that uses several preparatory variables to predict the outcome of a response variable. The goal of multiple linear regression (MLR) is to model the linear relationship between the explanatory (independent) variables and response (dependent) variable.
 
In essence, multiple regression is the extension of ordinary least-squares (OLS) regression that involves more than one explanatory variable.
 
Simple linear regression is a method that allows an analyst or statistician to make predictions about one variable based on the information that is known about another variable. Linear regression can only be used when one has two continuous variables—an independent variable and a dependent variable. The independent variable is the parameter that is used to calculate the dependent variable or outcome. A multiple regression model extends to several explanatory variables.
 
The multiple regression model is based on the following assumptions:
  1. Linearity: There is a linear relationship between the dependent variables and the independent variables.
  2. Correlation: The independent variables are not too highly correlated with each other.
  3. yi observations are selected independently and randomly from the population.
  4. Normal Distribution: Residuals should be normally distributed with a mean of 0 and variance σ.
When interpreting the results of multiple regression, beta coefficients are valid while holding all other variables constant ("all else equal"). The output from a multiple regression can be displayed horizontally as an equation, or vertically in table form. 
 
f_MLR 
 

Multiple Linear Regression Example 

 
Let's take the example of the IRIS dataset, you can directly import it from the sklearn dataset repository. Feel free to use any dataset, there some very good datasets available on kaggle and with Google Colab.
 
1. Using SkLearn
  1. from pandas import DataFrame    
  2. from sklearn import linear_model    
  3. import statsmodels.api as sm    
In the above code, we import the required python libraries.
  1. Stock_Market = {'Year': [2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016],    
  2.                 'Month': [12, 11,10,9,8,7,6,5,4,3,2,1,12,11,10,9,8,7,6,5,4,3,2,1],    
  3.                 'Interest_Rate': [2.75,2.5,2.5,2.5,2.5,2.5,2.5,2.25,2.25,2.25,2,2,2,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75],    
  4.                 'Unemployment_Rate': [5.3,5.3,5.3,5.3,5.4,5.6,5.5,5.5,5.5,5.6,5.7,5.9,6,5.9,5.8,6.1,6.2,6.1,6.1,6.1,5.9,6.2,6.2,6.1],    
  5.                 'Stock_Index_Price': [1464,1394,1357,1293,1256,1254,1234,1195,1159,1167,1130,1075,1047,965,943,958,971,949,884,866,876,822,704,719]            
  6.                 }    
In the above code, we are defining our data.
  1. df = DataFrame(Stock_Market,columns=['Year','Month','Interest_Rate','Unemployment_Rate','Stock_Index_Price'])    
  2.  
  3. X = df[['Interest_Rate','Unemployment_Rate']]    
  4. Y = df['Stock_Index_Price']   
In the above code, we are pre-processing the data.
  1. regr = linear_model.LinearRegression()    
  2. regr.fit(X, Y)    
In the above code, we are generating the model
  1. print('Intercept: \n', regr.intercept_)    Multiple Linear Regression using Python
  2. print('Coefficients: \n', regr.coef_)    
In the above code, we are printing the parameters of the generated model
 
the output that I am getting is :
Intercept: 1798.4039776258546
Coefficients: [ 345.54008701 -250.14657137] 
  1. # prediction with sklearn    
  2. New_Interest_Rate = 2.75    
  3. New_Unemployment_Rate = 5.3    
  4. print ('Predicted Stock Index Price: \n', regr.predict([[New_Interest_Rate ,New_Unemployment_Rate]]))   
In the above code, we are predicting the stock price corresponding to the given feature values.
  
MLR_SkLearn.py 
  1. from pandas import DataFrame  
  2. from sklearn import linear_model  
  3. import statsmodels.api as sm  
  4.   
  5. Stock_Market = {'Year': [2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2017,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016,2016],  
  6.                 'Month': [12, 11,10,9,8,7,6,5,4,3,2,1,12,11,10,9,8,7,6,5,4,3,2,1],  
  7.                 'Interest_Rate': [2.75,2.5,2.5,2.5,2.5,2.5,2.5,2.25,2.25,2.25,2,2,2,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75,1.75],  
  8.                 'Unemployment_Rate': [5.3,5.3,5.3,5.3,5.4,5.6,5.5,5.5,5.5,5.6,5.7,5.9,6,5.9,5.8,6.1,6.2,6.1,6.1,6.1,5.9,6.2,6.2,6.1],  
  9.                 'Stock_Index_Price': [1464,1394,1357,1293,1256,1254,1234,1195,1159,1167,1130,1075,1047,965,943,958,971,949,884,866,876,822,704,719]          
  10.                 }  
  11.                   
  12. df = DataFrame(Stock_Market,columns=['Year','Month','Interest_Rate','Unemployment_Rate','Stock_Index_Price'])  
  13.   
  14. X = df[['Interest_Rate','Unemployment_Rate']] # here we have 2 variables for multiple regression. If you just want to use one variable for simple linear regression, then use X = df['Interest_Rate'] for example.Alternatively, you may add additional variables within the brackets  
  15. Y = df['Stock_Index_Price']  
  16.    
  17. # with sklearn  
  18. regr = linear_model.LinearRegression()  
  19. regr.fit(X, Y)  
  20.   
  21. print('Intercept: \n', regr.intercept_)  
  22. print('Coefficients: \n', regr.coef_)  
  23.   
  24. # prediction with sklearn  
  25. New_Interest_Rate = 2.75  
  26. New_Unemployment_Rate = 5.3  
  27. print ('Predicted Stock Index Price: \n', regr.predict([[New_Interest_Rate ,New_Unemployment_Rate]]))    
Output
 
Intercept: 1798.4039776258546
Coefficients: [ 345.54008701 -250.14657137]
Predicted Stock Index Price: [1422.86238865]
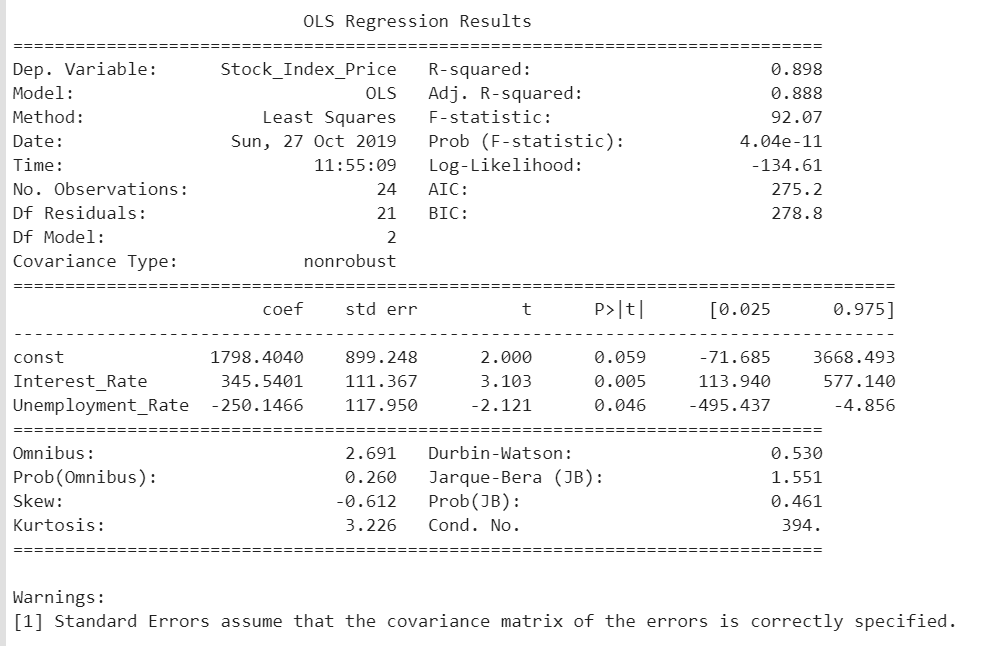
  1. print_model = model.summary()  
  2. print(print_model)  
Output 
 mlr
 

2. Using NumPy

  1. import numpy as np  
  2. import pandas as pd  
  3. import matplotlib.pyplot as plt  
  4. import seaborn as sns  
In the above code, we are importing the necessary libraries.
  1. my_data = pd.read_csv('home.txt',names=["size","bedroom","price"])  
In the above code, we are importing the data.
  1. #we need to normalize the features using mean normalization  
  2. my_data = (my_data - my_data.mean())/my_data.std()  
  3.   
  4. #setting the matrixes  
  5. X = my_data.iloc[:,0:2]  
  6. ones = np.ones([X.shape[0],1])  
  7. X = np.concatenate((ones,X),axis=1)  
  8.   
  9. y = my_data.iloc[:,2:3].values #.values converts it from pandas.core.frame.DataFrame to numpy.ndarray  
  10. theta = np.zeros([1,3])  
In the above code, we are preprocessing the data.
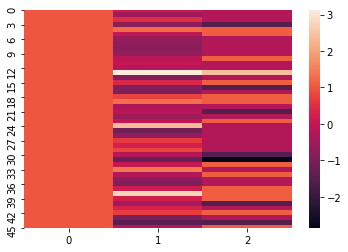
  1. sns.heatmap(X)  
Let us visualize the data using a heatmap.
heatmap 
  1. def computeCost(X,y,theta):  
  2.     tobesummed = np.power(((X @ theta.T)-y),2)  
  3.     return np.sum(tobesummed)/(2 * len(X))  
  4.   
  5. def gradientDescent(X,y,theta,iters,alpha):  
  6.     cost = np.zeros(iters)  
  7.     for i in range(iters):  
  8.         theta = theta - (alpha/len(X)) * np.sum(X * (X @ theta.T - y), axis=0)  
  9.         cost[i] = computeCost(X, y, theta)  
  10.       
  11.     return theta,cost  
In the above code, we are defining the methods for finding the cost and for gradient descent
  1. #set hyperparameters  
  2. alpha = 0.01  
  3. iters = 1000  
In the above code, we are setting the value for the hyperparameters.
  1. g,cost = gradientDescent(X,y,theta,iters,alpha)  
  2. print(g)  
  3.   
  4. finalCost = computeCost(X,y,g)  
  5. print(finalCost)  
In the above code, we are calling the methods for fitting the model
 
The output that I am getting is 
[[-1.10868761e-16 8.78503652e-01 -4.69166570e-02]] 0.13070336960771892
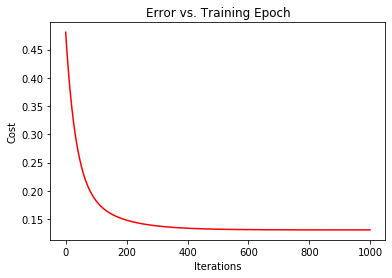
  1. fig, ax = plt.subplots()    
  2. ax.plot(np.arange(iters), cost, 'r')    
  3. ax.set_xlabel('Iterations')    
  4. ax.set_ylabel('Cost')    
  5. ax.set_title('Error vs. Training Epoch')    
In the above code, we are generating the graph of Error vs Training Epochs
 
output
 
 
MLR_NumPy.py 
  1. import numpy as np  
  2. import pandas as pd  
  3. import matplotlib.pyplot as plt  
  4. import seaborn as sns  
  5.   
  6. my_data = pd.read_csv('home.txt',names=["size","bedroom","price"])  
  7.   
  8. #we need to normalize the features using mean normalization  
  9. my_data = (my_data - my_data.mean())/my_data.std()  
  10.   
  11. #setting the matrixes  
  12. X = my_data.iloc[:,0:2]  
  13. ones = np.ones([X.shape[0],1])  
  14. X = np.concatenate((ones,X),axis=1)  
  15.   
  16. y = my_data.iloc[:,2:3].values #.values converts it from pandas.core.frame.DataFrame to numpy.ndarray  
  17. theta = np.zeros([1,3])  
  18.   
  19. sns.heatmap(X)  
  20.   
  21. #computecost  
  22. def computeCost(X,y,theta):  
  23.     tobesummed = np.power(((X @ theta.T)-y),2)  
  24.     return np.sum(tobesummed)/(2 * len(X))  
  25.   
  26. def gradientDescent(X,y,theta,iters,alpha):  
  27.     cost = np.zeros(iters)  
  28.     for i in range(iters):  
  29.         theta = theta - (alpha/len(X)) * np.sum(X * (X @ theta.T - y), axis=0)  
  30.         cost[i] = computeCost(X, y, theta)  
  31.       
  32.     return theta,cost  
  33.   
  34. #set hyper parameters  
  35. alpha = 0.01  
  36. iters = 1000  
  37.   
  38. g,cost = gradientDescent(X,y,theta,iters,alpha)  
  39. print(g)  
  40.   
  41. finalCost = computeCost(X,y,g)  
  42. print(finalCost)  
  43.   
  44. fig, ax = plt.subplots()    
  45. ax.plot(np.arange(iters), cost, 'r')    
  46. ax.set_xlabel('Iterations')    
  47. ax.set_ylabel('Cost')    
  48. ax.set_title('Error vs. Training Epoch')    
3. Using TensorFlow
  1. import matplotlib.pyplot as plt  
  2. import tensorflow as tf  
  3. import tensorflow.contrib.learn as skflow  
  4. from sklearn.utils import shuffle  
  5. import numpy as np  
  6. import pandas as pd  
  7. import seaborn as sns  
In the above code, we are importing the required libraries
  1. df = pd.read_csv("boston.csv", header=0)  
  2. print (df.describe())  
In the above code, we are importing the dataset. You can download the dataset from Kaggle
  1. sns.heatmap(df)  
Let us visualize the data.
heatmap1
 
  1. f, ax1 = plt.subplots()  
  2.   
  3. y = df['MEDV']  
  4.   
  5. for i in range (1,8):  
  6.     number = 420 + i  
  7.     ax1.locator_params(nbins=3)  
  8.     ax1 = plt.subplot(number)  
  9.     plt.title(list(df)[i])  
  10.     ax1.scatter(df[df.columns[i]],y) #Plot a scatter draw of the  datapoints  
  11. plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0)  
  12.   
  13. plt.show()  
Let us visualize each dataset column separately.
 
data
  1. X = tf.placeholder("float", name="X") # create symbolic variables  
  2. Y = tf.placeholder("float", name = "Y")  
In the above code, we are defining the actual trainable variables.
  1. with tf.name_scope("Model"):  
  2.   
  3.     w = tf.Variable(tf.random_normal([2], stddev=0.01), name="b0") # create a shared variable  
  4.     b = tf.Variable(tf.random_normal([2], stddev=0.01), name="b1") # create a shared variable  
  5.       
  6.     def model(X, w, b):  
  7.         return tf.multiply(X, w) + b # We just define the line as X*w + b0    
  8.   
  9.     y_model = model(X, w, b)  
In the above code, we are defining the model.
  1. with tf.name_scope("CostFunction"):  
  2.     cost = tf.reduce_mean(tf.pow(Y-y_model, 2)) # use sqr error for cost function  
  3.   
  4. train_op = tf.train.AdamOptimizer(0.001).minimize(cost)  
In the above code, we are defining the cost function and the cost optimizer function.
  1. sess = tf.Session()  
  2. init = tf.initialize_all_variables()  
  3. tf.train.write_graph(sess.graph, '/home/bonnin/linear2','graph.pbtxt')  
  4. cost_op = tf.summary.scalar("loss", cost)  
  5. merged = tf.summary.merge_all()  
  6. sess.run(init)  
  7. writer = tf.summary.FileWriter('/home/bonnin/linear2', sess.graph)  
In the above code, we create the garph file which can be used to visualize the model on TensorBoard.
  1. xvalues = df[[df.columns[2], df.columns[4]]].values.astype(float)  
  2. yvalues = df[df.columns[12]].values.astype(float)  
  3. b0temp=b.eval(session=sess)  
  4. b1temp=w.eval(session=sess)  
In the above code, we are making sure that the values are accesible to us even after the session ends.
  1. for a in range (1,50):  
  2.     cost1=0.0  
  3.     for i, j in zip(xvalues, yvalues):     
  4.         sess.run(train_op, feed_dict={X: i, Y: j})   
  5.         cost1+=sess.run(cost, feed_dict={X: i, Y: i})/506.00  
  6.     xvalues, yvalues = shuffle (xvalues, yvalues)  
  7.     print ("Cost over iterations",cost1)  
  8.     b0temp=b.eval(session=sess)  
  9.     b1temp=w.eval(session=sess)   
In the above code, we are doing training.
  1. print("the final equation comes out to be", b0temp,"+",b1temp,"*X","\n Cost :",cost1)      
In the above code, we are printing the model and the final cost.
 
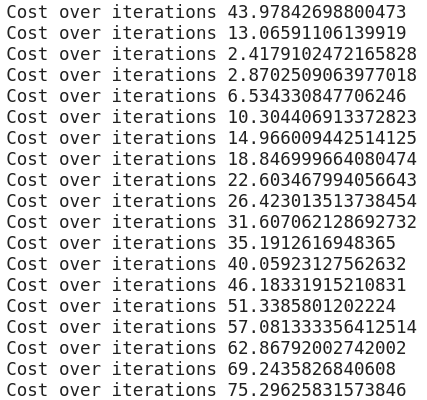
The output that I am getting is
the final equation comes out to be [4.7545404 7.7991614] + [1.0045488 7.807921 ] *X
Cost: 75.29625831573846
 
training
 
MLR_TensorFlow.py 
  1. import tensorflow as tf  
  2. import tensorflow.contrib.learn as skflow  
  3. from sklearn.utils import shuffle  
  4. import numpy as np  
  5. import pandas as pd  
  6.   
  7. df = pd.read_csv("boston.csv", header=0)  
  8. print (df.describe())  
  9.   
  10. f, ax1 = plt.subplots()  
  11. import seaborn as sns  
  12. sns.heatmap(df)  
  13.   
  14. y = df['MEDV']  
  15.   
  16. for i in range (1,8):  
  17.     number = 420 + i  
  18.     ax1.locator_params(nbins=3)  
  19.     ax1 = plt.subplot(number)  
  20.     plt.title(list(df)[i])  
  21.     ax1.scatter(df[df.columns[i]],y) #Plot a scatter draw of the  datapoints  
  22. plt.tight_layout(pad=0.4, w_pad=0.5, h_pad=1.0)  
  23.   
  24. plt.show()  
  25.   
  26. X = tf.placeholder("float", name="X") # create symbolic variables  
  27. Y = tf.placeholder("float", name = "Y")  
  28.   
  29. with tf.name_scope("Model"):  
  30.   
  31.     w = tf.Variable(tf.random_normal([2], stddev=0.01), name="b0") # create a shared variable  
  32.     b = tf.Variable(tf.random_normal([2], stddev=0.01), name="b1") # create a shared variable  
  33.       
  34.     def model(X, w, b):  
  35.         return tf.multiply(X, w) + b # We just define the line as X*w + b0    
  36.   
  37.     y_model = model(X, w, b)  
  38.   
  39. with tf.name_scope("CostFunction"):  
  40.     cost = tf.reduce_mean(tf.pow(Y-y_model, 2)) # use sqr error for cost function  
  41.   
  42. train_op = tf.train.AdamOptimizer(0.001).minimize(cost)  
  43.   
  44.   
  45. sess = tf.Session()  
  46. init = tf.initialize_all_variables()  
  47. tf.train.write_graph(sess.graph, '/home/bonnin/linear2','graph.pbtxt')  
  48. cost_op = tf.summary.scalar("loss", cost)  
  49. merged = tf.summary.merge_all()  
  50. sess.run(init)  
  51. writer = tf.summary.FileWriter('/home/bonnin/linear2', sess.graph)  
  52.   
  53. xvalues = df[[df.columns[2], df.columns[4]]].values.astype(float)  
  54. yvalues = df[df.columns[12]].values.astype(float)  
  55. b0temp=b.eval(session=sess)  
  56. b1temp=w.eval(session=sess)  
  57.   
  58. for a in range (1,50):  
  59.     cost1=0.0  
  60.     for i, j in zip(xvalues, yvalues):     
  61.         sess.run(train_op, feed_dict={X: i, Y: j})   
  62.         cost1+=sess.run(cost, feed_dict={X: i, Y: i})/506.00  
  63.     xvalues, yvalues = shuffle (xvalues, yvalues)  
  64.     print ("Cost over iterations",cost1)  
  65.     b0temp=b.eval(session=sess)  
  66.     b1temp=w.eval(session=sess)   
  67.   
  68. print("the final equation comes out to be", b0temp,"+",b1temp,"*X")   

Conclusion

 
In this chapter, you studied multiple linear regression.
 
In the next chapter, you will study the decision tree.
Author
Rohit Gupta
65 27.3k 3m
Next » Machine Learninig: Decision Tree

©2024 C# Corner.