Machine Learning: KNN- K-Nearest Neighbors

Introduction

 
In the previous chapter, we studied k-means clustering. 
 
In this chapter, we will learn k-nearest neighbor.
 
Note: ifyou can correlate anything with yourself or your life, there are greater chances of understanding the concept. So try to understand everything by relating it to humans.
 

What is K nearest neighbor used for?

 
KNN can be used for both classification and regression predictive problems. However, it is more widely used in classification problems in the industry. k-NN is often used in search applications where you are looking for “similar” items; that is when your task is some form of “find items similar to this one”. We use k-NN when we have fewer than 20 features (attributes) per instance, typically normalized​ or we have a lot of training data.
 

What is KNN?

 
KNN is a non-parametric, lazy learning algorithm; i.e. it does not make any assumptions on the underlying data, and also there is no explicit training phase or it is very minimal.
 
k-NN is all about finding the next data point(s) which is at the minimum distance from the current data point and to club all into one class.
 
k is the max value of data point(s) that can be clubbed under a given class.
 
To find the distance we use employ various algorithms like Euclidean Distance, Hamming Distance, Manhattan Distance, Minkowski Distance, etc.
 
For example, 1-NN means that we have to generate a model that will have classes based on the data point which is at the least distance. Similarily, 2-NN means that we have to generate a model that will have classes based on the 2 data points with the least distances.
 
The algorithm of k-NN or K-Nearest Neighbors is:
  1. Computes the distance between the new data point with every training example.
  2. For computing, distance measures such as Euclidean distance, Hamming distance or Manhattan distance will be used.
  3. The model picks K entries in the database which are closest to the new data point.
  4. Then it does the majority vote i.e the most common class/label among those K entries will be the class of the new data point.
Steps involved in the processing and generating a model
  1. Decide on your similarity or distance metric.
  2. Split the original labeled dataset into training and test data.
  3. Pick an evaluation metric.
  4. Decide upon the value of k. Here k refers to the number of closest neighbors we will consider while doing the majority voting of target labels.
  5. Run k-NN a few times, changing k and checking the evaluation measure.
  6. In each iteration, k neighbors vote, majority vote wins and becomes the ultimate prediction
  7. Optimize k by picking the one with the best evaluation measure.
  8. Once you’ve chosen k, use the same training set and now create a new test set with the people’s wages and incomes that you have no labels for, and want to predict.
Steps involved in selecting the value for K
  1. Determined experimentally​
  2. Start with k=1 and use a test set to validate the error rate of the classifier​
  3. Repeat with k=k+2​
  4. Choose the value of k for which the error rate is minimum​
    Note: k should be an odd number to avoid ties​

1-NN

 
1nn
 

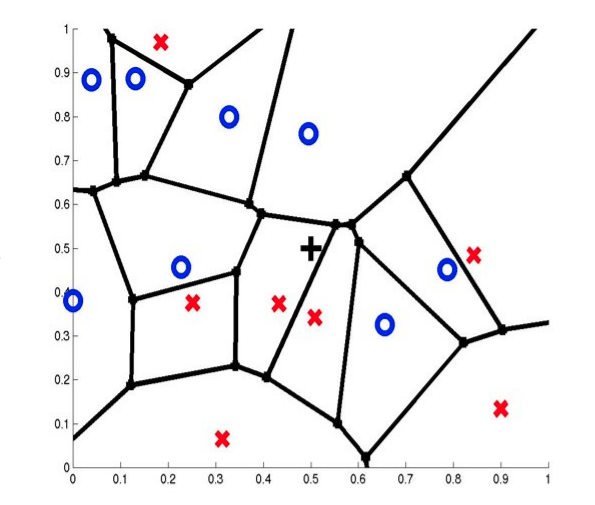
3-NN

 
3nn 
 

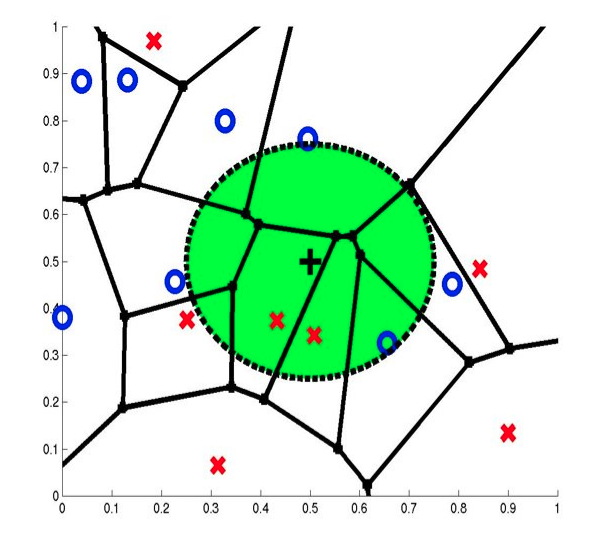
7-NN

 
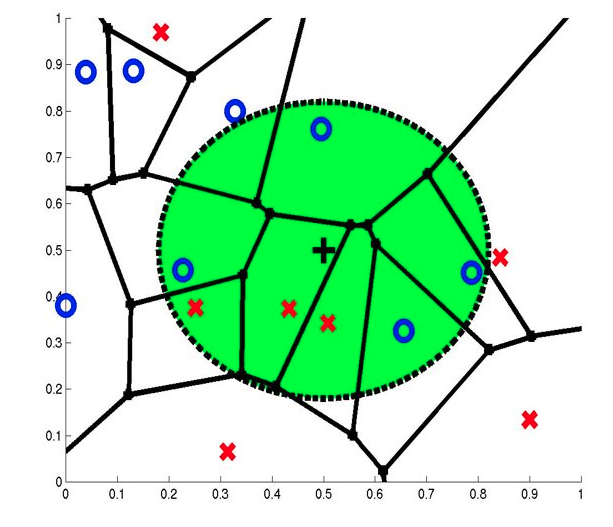
7nn 
 

KNN vs K-Means Clustering

 
  k-NN k-Means
Types
Supervised
Unsupervised
What is K?
 Number of closest neighbors to look at
Number of centroids
Calculation of prediction error possible
 Yes
 No
Optimization is done using what?
Cross-validation and confusion matrix
 Elbow method and the silhouette method
Algorithm convergences
 When all observations classified at the desired accuracy
When cluster membership doesn't change anymore
Complexity
 Training: O(Dimensions/Features)
Test: O (Number of Observations)
 O (Number of points * Number of Clusters * Number of iterations * number of attributes)
 

Curse of Dimensionality

 
Imagine instances described by 20 features (attributes) but only 3 are relevant to the target function​. Curse of dimensionality means that nearest neighbor can be easily misled when instance space is high-dimensional​ and is dominated by a large number of irrelevant features​.
 
A solution to this can be
  1. Stretch j-th axis by weight zj, where z1,…,zn chosen to minimize prediction error (weight different features differently)​
  2. Use cross-validation to automatically choose weights z1,…,zn ​
  3. Note setting zj to zero eliminates this dimension altogether (feature subset selection)​
  4. PCA​

Assumptions of KNN

  1. k-NN performs much better if all of the data have the same scale
  2. k-NN works well with a small number of input variables (p) but struggles when the number of inputs is very large
  3. k-NN makes no assumptions about the functional form of the problem is solved
Euclidean distance
 
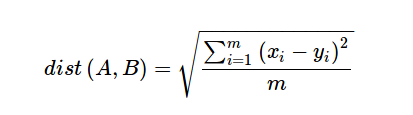
euclidean 
 
Manhattan Distance
 
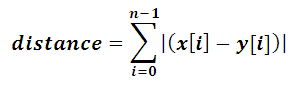
manhattan 
 
Chi-Square Distance
 
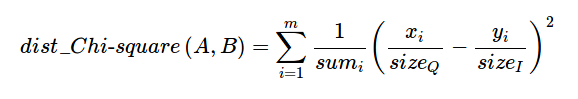
ch-sqaure 
 
Correlation Distance
 
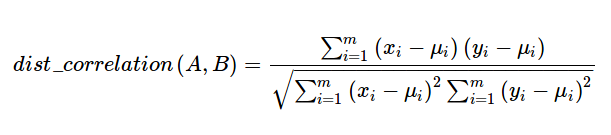
correlation 
 
Hamming Distance
 
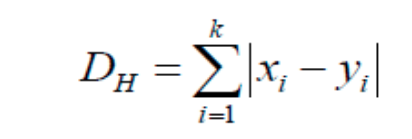
hamming 
 
Minkowsky Distance
 
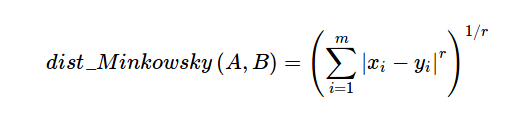
minkowsky 
 

KNN using an example

 
Let us understand how k-NN really works. For that let's take a dummy dataset.
 
data = [
       [65.75, 112.99],
       [71.52, 136.49],
       [69.40, 153.03],
       [68.22, 142.34], 
       [67.79, 144.30],
       [68.70, 123.30],
       [69.80, 141.49],
       [70.01, 136.46],
       [67.90, 112.37],
       [66.49, 127.45],
    ]
 
In the above example, the data is of the form [feature, target].
 
Assuming the value of k to be 3 i.e. 3-NN, let's try to find the prediction for feature value "60".
 
So the 3 nearest neighbors would be 
a. 65.75 with a distance value 5.75
b. 66.49 with a distance value 6.49
c. 67.79 with a distance value 7.79
 
And hence the predicted value will be 128.25.
 
Similarly, let's take another dataset
 
data = [   
    [22, 1],   
    [23, 1],   
    [21, 1],   
    [18, 1],   
    [19, 1],   
    [25, 0],   
    [27, 0],   
    [29, 0],   
    [31, 0],   
    [45, 0],   
]
 
In the above example, the data is of the form [feature, target].
 
Assuming the value of k to be 3 i.e. 3-NN, let's try to find the prediction for feature value "33".
 
So the 3 nearest neighbors would be 
a. 31 with a distance value 2.0
b. 29 with a distance value 4.0
c. 27 with a distance value 6.0
 
And hence the predicted value will be 0.
 

Python Implementation of Decision Tree

 
Let's take the example of the MNIST dataset, you can directly import it from the sklearn dataset repository. Feel free to use any dataset, there are some very good datasets available on kaggle and with Google Colab.

1. From Scratch

 
Here, I will be using some dummy data. You can use and practice on any kind of data
  1. from collections import Counter    
  2. import math  
In the above code, we are exporting the required libraries.
  1. def knn(data, query, k, distance_fn, choice_fn):    
  2.     neighbor_distances_and_indices = []    
  3.         
  4.     # 3. For each example in the data    
  5.     for index, example in enumerate(data):    
  6.         # 3.1 Calculate the distance between the query example and the current    
  7.         # example from the data.    
  8.         distance = distance_fn(example[:-1], query)    
  9.             
  10.         # 3.2 Add the distance and the index of the example to an ordered collection    
  11.         neighbor_distances_and_indices.append((distance, index))    
  12.         
  13.     # 4. Sort the ordered collection of distances and indices from    
  14.     # smallest to largest (in ascending order) by the distances    
  15.     sorted_neighbor_distances_and_indices = sorted(neighbor_distances_and_indices)    
  16.         
  17.     # 5. Pick the first K entries from the sorted collection    
  18.     k_nearest_distances_and_indices = sorted_neighbor_distances_and_indices[:k]    
  19.         
  20.     # 6. Get the labels of the selected K entries    
  21.     k_nearest_labels = [data[i][1] for distance, i in k_nearest_distances_and_indices]    
  22.     
  23.     # 7. If regression (choice_fn = mean), return the average of the K labels    
  24.     # 8. If classification (choice_fn = mode), return the mode of the K labels    
  25.     return k_nearest_distances_and_indices , choice_fn(k_nearest_labels)   
In the above code, we have created a function that will perform all the required tasks to result out a k-NN based model
  1. #function to calculate the mean used in case of regression  
  2. def mean(labels):    
  3.     return sum(labels) / len(labels)    
  4.    
  5. #function to calculate the mode used in case of classification   
  6. def mode(labels):    
  7.     return Counter(labels).most_common(1)[0][0]    
  8.     
  9. #function to calculate the distance between two data points  
  10. def euclidean_distance(point1, point2):    
  11.     sum_squared_distance = 0    
  12.     for i in range(len(point1)):    
  13.         sum_squared_distance += math.pow(point1[i] - point2[i], 2)    
  14.     return math.sqrt(sum_squared_distance) 
The above code lists down all the auxiliary functions used during the program
  1. # Regression Data   
  2.     #    
  3.     # Column 0: height (inches)   
  4.     # Column 1: weight (pounds)   
  5.     '''    
  6.     reg_data = [    
  7.        [65.75, 112.99],    
  8.        [71.52, 136.49],    
  9.        [69.40, 153.03],    
  10.        [68.22, 142.34],    
  11.        [67.79, 144.30],    
  12.        [68.70, 123.30],    
  13.        [69.80, 141.49],    
  14.        [70.01, 136.46],    
  15.        [67.90, 112.37],    
  16.        [66.49, 127.45],    
  17.     ]   
The above code, declares the dummy regression data, in the above data column 0 signifies height and column 1 signifies weight
  1. reg_query = [60]    
  2. reg_k_nearest_neighbors, reg_prediction = knn(    
  3. reg_data, reg_query, k=3, distance_fn=euclidean_distance, choice_fn=mean    
  4. )    
  5. print(reg_k_nearest_neighbors, reg_prediction) 
In the above code, we will generate a model, and then based on that model will  predict the weight for a person with a height of 60
  1. '''''''  
  2. # Classification Data  
  3. #   
  4. # Column 0: age  
  5. # Column 1: likes pineapple  
  6. '''    
  7. clf_data = [    
  8.     [22, 1],    
  9.     [23, 1],    
  10.     [21, 1],    
  11.     [18, 1],    
  12.     [19, 1],    
  13.     [25, 0],    
  14.     [27, 0],    
  15.     [29, 0],    
  16.     [31, 0],    
  17.     [45, 0],    
  18. ] 
The above code, declares the dummy data for classification based problem, where column 0 signifies age and column 1 signifies if a person like pineapple or not
  1. clf_query = [33]    
  2. clf_k_nearest_neighbors, clf_prediction = knn(    
  3.               clf_data, clf_query, k=3, distance_fn=euclidean_distance,choice_fn=mode) 
  4. print(clf_k_nearest_neighbors, clf_prediction) 
In the above code, we first create a model, and based on that model, we predict if a 33 years old person likes pineapple or not.
 

scratch_knn.py

  1. from collections import Counter  
  2. import math  
  3.   
  4. def knn(data, query, k, distance_fn, choice_fn):  
  5.     neighbor_distances_and_indices = []  
  6.       
  7.     # 3. For each example in the data  
  8.     for index, example in enumerate(data):  
  9.         # 3.1 Calculate the distance between the query example and the current  
  10.         # example from the data.  
  11.         distance = distance_fn(example[:-1], query)  
  12.           
  13.         # 3.2 Add the distance and the index of the example to an ordered collection  
  14.         neighbor_distances_and_indices.append((distance, index))  
  15.       
  16.     # 4. Sort the ordered collection of distances and indices from  
  17.     # smallest to largest (in ascending order) by the distances  
  18.     sorted_neighbor_distances_and_indices = sorted(neighbor_distances_and_indices)  
  19.       
  20.     # 5. Pick the first K entries from the sorted collection  
  21.     k_nearest_distances_and_indices = sorted_neighbor_distances_and_indices[:k]  
  22.       
  23.     # 6. Get the labels of the selected K entries  
  24.     k_nearest_labels = [data[i][1] for distance, i in k_nearest_distances_and_indices]  
  25.   
  26.     # 7. If regression (choice_fn = mean), return the average of the K labels  
  27.     # 8. If classification (choice_fn = mode), return the mode of the K labels  
  28.     return k_nearest_distances_and_indices , choice_fn(k_nearest_labels)  
  29.   
  30. def mean(labels):  
  31.     return sum(labels) / len(labels)  
  32.   
  33. def mode(labels):  
  34.     return Counter(labels).most_common(1)[0][0]  
  35.   
  36. def euclidean_distance(point1, point2):  
  37.     sum_squared_distance = 0  
  38.     for i in range(len(point1)):  
  39.         sum_squared_distance += math.pow(point1[i] - point2[i], 2)  
  40.     return math.sqrt(sum_squared_distance)  
  41.   
  42. def main():  
  43.     ''''' 
  44.     # Regression Data 
  45.     #  
  46.     # Column 0: height (inches) 
  47.     # Column 1: weight (pounds) 
  48.     '''  
  49.     reg_data = [  
  50.        [65.75, 112.99],  
  51.        [71.52, 136.49],  
  52.        [69.40, 153.03],  
  53.        [68.22, 142.34],  
  54.        [67.79, 144.30],  
  55.        [68.70, 123.30],  
  56.        [69.80, 141.49],  
  57.        [70.01, 136.46],  
  58.        [67.90, 112.37],  
  59.        [66.49, 127.45],  
  60.     ]  
  61.       
  62.     # Question:  
  63.     # Given the data we have, what's the best-guess at someone's weight if they are 60 inches tall?  
  64.     reg_query = [60]  
  65.     reg_k_nearest_neighbors, reg_prediction = knn(  
  66.         reg_data, reg_query, k=3, distance_fn=euclidean_distance, choice_fn=mean  
  67.     )  
  68.     print(reg_k_nearest_neighbors, reg_prediction)  
  69.       
  70.     ''''' 
  71.     # Classification Data 
  72.     #  
  73.     # Column 0: age 
  74.     # Column 1: likes pineapple 
  75.     '''  
  76.     clf_data = [  
  77.        [22, 1],  
  78.        [23, 1],  
  79.        [21, 1],  
  80.        [18, 1],  
  81.        [19, 1],  
  82.        [25, 0],  
  83.        [27, 0],  
  84.        [29, 0],  
  85.        [31, 0],  
  86.        [45, 0],  
  87.     ]  
  88.     # Question:  
  89.     # Given the data we have, does a 33 year old like pineapples on their pizza?  
  90.     clf_query = [33]  
  91.     clf_k_nearest_neighbors, clf_prediction = knn(  
  92.         clf_data, clf_query, k=3, distance_fn=euclidean_distance, choice_fn=mode  
  93.     )  
  94.     print(clf_k_nearest_neighbors, clf_prediction)  
  95.   
  96. if __name__ == '__main__':  
  97.     main() 
The output that I got is:
 
Regression case:
Neighbors: [(5.75, 0), (6.489999999999995, 9), (7.790000000000006, 4)]
Prediction: 128.24666666666667
 
Classification case:
Neighbors: [(2.0, 8), (4.0, 7), (6.0, 6)]
Prediction: 0
 

2. Using SkLearn

 
In sklean, we have KNeighnotsClassifier class, used for implementing k-NN
 

knn_sklearn.py

  1. X = [[0], [1], [2], [3]]  
  2. y = [0, 0, 1, 1]  
  3. from sklearn.neighbors import KNeighborsClassifier  
  4. neigh = KNeighborsClassifier(n_neighbors=2)  
  5. neigh.fit(X, y)   
  6. print(neigh.predict([[4.567]]))
  7. print(neigh.predict_proba([[4.567]]))
In the above code, we create a dummy data, which is then passed to the classifier, to get the predicted value and predicting probability corresponding to 4.567
 
The output that I got is
Predicted value: [1]
Predicting Probability: [[0. 1.]]
 

3. Using TensorFlow

 
Here I will be using the MNSIT cloth dataset. 
  1. from __future__ import print_function    
  2.     
  3. import numpy as np    
  4. import tensorflow as tf   
In the above code, we are importing all the required libraries.
 
In the below code, I have commented on Line numbers 41 and 42, you can uncomment those if you want to see the complete output.
 

knn_tensorflow.py

  1. from __future__ import print_function  
  2.   
  3. import numpy as np  
  4. import tensorflow as tf  
  5.   
  6. # Import MNIST data  
  7. from tensorflow.examples.tutorials.mnist import input_data  
  8. mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)  
  9.   
  10. # In this example, we limit mnist data  
  11. Xtr, Ytr = mnist.train.next_batch(5000) #5000 for training (nn candidates)  
  12. Xte, Yte = mnist.test.next_batch(200) #200 for testing  
  13.   
  14. # tf Graph Input  
  15. xtr = tf.placeholder("float", [None, 784])  
  16. xte = tf.placeholder("float", [784])  
  17.   
  18. # Nearest Neighbor calculation using L1 Distance  
  19. # Calculate L1 Distance  
  20. distance = tf.reduce_sum(tf.abs(tf.add(xtr, tf.negative(xte))), reduction_indices=1)  
  21. # Prediction: Get min distance index (Nearest neighbor)  
  22. pred = tf.arg_min(distance, 0)  
  23.   
  24. accuracy = 0.  
  25.   
  26. # Initialize the variables (i.e. assign their default value)  
  27. init = tf.global_variables_initializer()  
  28.   
  29. # Start training  
  30. with tf.Session() as sess:  
  31.   
  32.     # Run the initializer  
  33.     sess.run(init)  
  34.   
  35.     # loop over test data  
  36.     for i in range(len(Xte)):  
  37.         # Get nearest neighbor  
  38.         nn_index = sess.run(pred, feed_dict={xtr: Xtr, xte: Xte[i, :]})  
  39.         # Get nearest neighbor class label and compare it to its true label  
  40.           
  41.         #print("Test", i, "Prediction:", np.argmax(Ytr[nn_index]), \  
  42.          #   "True Class:", np.argmax(Yte[i]))  
  43.         # Calculate accuracy  
  44.         if np.argmax(Ytr[nn_index]) == np.argmax(Yte[i]):  
  45.             accuracy += 1./len(Xte)  
  46.     print("Done!")  
  47.     print("Accuracy:", accuracy) 
The output that I got is
 
Accuracy: 0.9450000000000007
 

Conclusion

 
In this chapter, we studied KNN i.e. K-Nearest Neighbours.
 
In the next chapter, we will study the support vector machine.
Author
Rohit Gupta
65 27.3k 3m
Next » Machine Learning: Support Vector Machine

©2024 C# Corner.